
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 任作一条与两条坐标轴都不垂直的直线,与椭圆
任作一条与两条坐标轴都不垂直的直线,与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 的周长为8,当直线
的周长为8,当直线![]() 的斜率为
的斜率为![]() 时,
时, ![]() 与
与![]() 轴垂直.
轴垂直.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在![]() 轴上是否存在定点
轴上是否存在定点![]() ,总能使
,总能使![]() 平分
平分![]() ?说明理由.
?说明理由.
科目:高中数学 来源: 题型:
【题目】某工程设备租赁公司为了调查A,B两种挖掘机的出租情况,现随机抽取了这两种挖掘机各100台,分别统计了每台挖掘机在一个星期内的出租天数,统计数据如下表:

(I)根据这个星期的统计数据,将频率视为概率,求该公司一台A型挖掘机,一台B型挖掘机一周内合计出租天数恰好为4天的概率;
(II)如果A,B两种挖掘机每台每天出租获得的利润相同,该公司需要从A,B两种挖掘机中购买一台,请你根据所学的统计知识,给出建议应该购买哪一种类型,并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
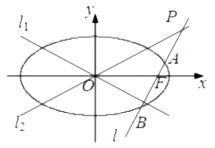
【题目】已知椭圆![]() 方程为
方程为![]() ,双曲线
,双曲线![]() 的两条渐近线分别为
的两条渐近线分别为![]() ,
, ![]() ,过椭圆
,过椭圆![]() 的右焦点作直线
的右焦点作直线![]() ,使
,使![]() ,又
,又![]() 与
与![]() 交于点
交于点![]() ,设直线
,设直线![]() 与椭圆
与椭圆![]() 的两个交点由上至下依次为
的两个交点由上至下依次为![]() ,
, ![]() .
.
(1)若![]() 与
与![]() 所成的锐角为
所成的锐角为![]() ,且双曲线的焦距为4,求椭圆
,且双曲线的焦距为4,求椭圆![]() 的方程;
的方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孝感市及周边地区的市民游玩又添新去处啦!孝感熙凤水乡旅游度假区于2017年10月1日正式对外开放.据统计,从2017年10月1日到10月7日参观孝感市熙凤水乡旅游度假区的人数如表所示:
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数(万) | 11 | 13 | 8 | 9 | 7 | 8 | 10 |
(1)把这7天的参观人数看成一个总体,求该总体的众数和平均数(精确到0.1);
(2)用简单随机抽样方法从10月1日到10月4日中抽取2天,它们的参观人数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过1万的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,且过点
,且过点![]() .直线
.直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求![]() 的面积的最大值;
的面积的最大值;
(Ⅲ)设直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .判断
.判断![]() ,
, ![]() 大小关系,并加以证明.
大小关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com