
【题目】设数列![]() 是各项均为正数的等比数列,其前
是各项均为正数的等比数列,其前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设有正整数![]() ,使得
,使得![]() 成等差数列,求
成等差数列,求![]() 的值;
的值;
(3)设![]() ,对于给定的
,对于给定的![]() ,求三个数
,求三个数![]() 经适当排序后能构成等差数列的充要条件.
经适当排序后能构成等差数列的充要条件.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 经适当排序后能构成等差数列的充要条件为
经适当排序后能构成等差数列的充要条件为![]()
【解析】【试题分析】(1)依据题设条件建立方程组,运用等比数列的性质求出![]() 求出等比
求出等比![]() ,求得通项公式
,求得通项公式![]() ;(2)依据题设
;(2)依据题设![]() 成等差数列,建立方程
成等差数列,建立方程![]() ,得到
,得到![]() ,也即
,也即![]() .由此推知
.由此推知![]() 中有且只有一个等于1,借助正整数
中有且只有一个等于1,借助正整数![]() 满足
满足![]() ,从而推知
,从而推知![]() ,求出
,求出![]() .
.
(3)按照题设要求将条件“![]() 经适当排序后能构成等差数列”分为三类
经适当排序后能构成等差数列”分为三类![]() 进行分析推证:
进行分析推证:
解:(1)因为数列![]() 是各项均为正数的等比数列,所以设数列
是各项均为正数的等比数列,所以设数列![]() 的公比为
的公比为![]() ,且
,且![]() .
.
又![]() ,且
,且![]() ,所以
,所以![]() .
.
又因为![]() ,所以
,所以![]() ,解得
,解得![]() ,所以
,所以![]() .
.
(2)因为![]() 成等差数列,所以
成等差数列,所以![]() ,即
,即![]() .
.
所以, ![]() .
.
故![]() 中有且只有一个等于1.
中有且只有一个等于1.
因为正整数![]() 满足
满足![]() ,所以
,所以![]() ,得
,得![]() .
.
(3)设![]() 经适当排序后能构成等差数列.
经适当排序后能构成等差数列.
①若![]() ,则
,则![]() ,当且仅当
,当且仅当![]() ,当且仅当
,当且仅当![]() .
.
因为正整数![]() 满足
满足![]() ,当且仅当
,当且仅当![]() ,且
,且![]() ,
,
所以![]() ,
, ![]() .当且仅当
.当且仅当![]() ,即
,即![]() .
.
②若![]() ,则
,则![]() ,所以
,所以![]() (*).
(*).
因为![]() ,
,
所以![]() 与
与![]() 都为偶数,而5是奇数,所以,等式(*)不成立,
都为偶数,而5是奇数,所以,等式(*)不成立,
从而等式![]() 不成立,
不成立,
③若![]() ,则同②可知,该等式也不成立.
,则同②可知,该等式也不成立.
综合①②③,得![]() .
.
设![]() ,则
,则![]() 为
为![]() ,即
,即![]() .
.
调整顺序后易知![]() 成等差数列.
成等差数列.
综上所述, ![]() 经适当排序后能构成等差数列的充要条件为
经适当排序后能构成等差数列的充要条件为![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】已知:椭圆 ![]() (a>b>0),过点
(a>b>0),过点 ![]() ,
, ![]() 的直线倾斜角为
的直线倾斜角为 ![]() ,原点到该直线的距离为
,原点到该直线的距离为 ![]() .
.
(1)求椭圆的方程;
(2)斜率大于零的直线过 ![]() 与椭圆交于E,F两点,若
与椭圆交于E,F两点,若 ![]() ,求直线EF的方程.
,求直线EF的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z的实部和虚部都是整数,
(1)若复数z为纯虚数,且|z﹣1|=|﹣1+i|,求复数z;
(2)若复数z满足z+ ![]() 是实数,且1<z+
是实数,且1<z+ ![]() ≤6,求复数z.
≤6,求复数z.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市理论预测2007年到2011年人口总数与年份的关系如表所示
年份2007+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据表提供的数据,求最小二乘法求出y关于x的线性回归方程;
(2)据此估计2012年该城市人口总数.
参考公式: 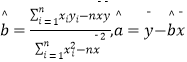 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在近30天内每件的销售价格P(元)与时间t(天)的函数关系是P= ![]() ,该商场的日销售量Q=﹣t+40(0<t≤30,t∈N),求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天.
,该商场的日销售量Q=﹣t+40(0<t≤30,t∈N),求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知6只小白鼠有1只被病毒感染,需要通过对其化验病毒![]() 来确定是否感染.下面是两种化验方案:方案甲:逐个化验,直到能确定感染为止.方案乙:将6只分为两组,每组三个,并将它们混合在一起化验,若存在病毒
来确定是否感染.下面是两种化验方案:方案甲:逐个化验,直到能确定感染为止.方案乙:将6只分为两组,每组三个,并将它们混合在一起化验,若存在病毒![]() ,则表明感染在这三只当中,然后逐个化验,直到确定感染为止;若结果不含病毒
,则表明感染在这三只当中,然后逐个化验,直到确定感染为止;若结果不含病毒![]() ,则在另外一组中逐个进行化验.
,则在另外一组中逐个进行化验.
(1)求依据方案乙所需化验恰好为2次的概率.
(2)首次化验化验费为10元,第二次化验化验费为8元,第三次及其以后每次化验费都是6元,列出方案甲所需化验费用的分布列,并估计用方案甲平均需要体验费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com