
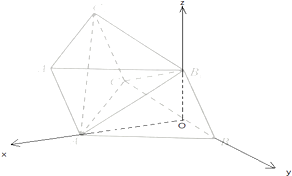
【题目】如图,已知斜三棱柱ABC﹣A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°. 
(1)求证:BC⊥AB1;
(2)若AB=2,AB1= ![]() ,求二面角C﹣AB1﹣C1(锐角)的余弦值.
,求二面角C﹣AB1﹣C1(锐角)的余弦值.
【答案】
(1)证明:∵四边形BB1C1C是菱形,∠CBB1=60°,
∴△BB1C是等边三角形,
取BC的中点为O,连结OA,OB,则BC⊥OB1,
又∵△ABC是等边三角形,∴BC⊥OA,
∵OA∩OB1,∴BC⊥平面AOB1,
∵AB1平面AOB1,∴BC⊥AB1.
(2)解:∵△ABC和△BB1C是全等的等边三角形,AB=2,
∴OA=OB1= ![]() ,
,
又∵AB1= ![]() ,∴
,∴ ![]() ,∴OB1⊥OA,
,∴OB1⊥OA,
又∵OB1⊥BC,∴OB1⊥平面ABC,
分别以OA,OB,OB1所在的直线作为x,y,z轴,建立空间直角坐标系,
则A( ![]() ),B(0,1,0),C(0,﹣1,0),
),B(0,1,0),C(0,﹣1,0),
![]() =(0,﹣1,﹣
=(0,﹣1,﹣ ![]() ),
), ![]() =(﹣
=(﹣ ![]() ),
), ![]() =(0,﹣2,0),
=(0,﹣2,0), ![]() =(﹣
=(﹣ ![]() ,﹣1,0),
,﹣1,0),
设 ![]() =(x,y,z)是平面C1AB1的一个法向量,
=(x,y,z)是平面C1AB1的一个法向量,
则  ,取x=1,得
,取x=1,得 ![]() =(1,0,1),
=(1,0,1),
设 ![]() =(a,b,c)是平面CAB1的一个法向量,
=(a,b,c)是平面CAB1的一个法向量,
则 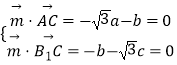 ,取a=1,得
,取a=1,得 ![]() =(1,﹣
=(1,﹣ ![]() ,1),
,1),
cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() ,
,
∴二面角C﹣AB1﹣C1(锐角)的余弦值为 ![]() .
.
【解析】(1)推导出△BB1C是等边三角形,取BC的中点为O,则BC⊥OB1 , 由△ABC是等边三角形,得BC⊥OA,从而BC⊥平面AOB1 , 由此能证明BC⊥AB1 . (2)分别以OA,OB,OB1所在的直线作为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角C﹣AB1﹣C1(锐角)的余弦值.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号 | 1 | 2 | 3 | 4 | 5 |
储蓄存款 | 6 | 7 | 8 | 9 | 10 |
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)用所求回归方程预测该地区2015年![]() 的人民币储蓄存款.
的人民币储蓄存款.
附:回归方程![]() 中,
中, 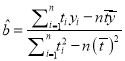 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中学校在2015年的一次体能测试中,规定所有男生必须依次参加50米跑、立定跳远和一分钟的引体向上三项测试,只有三项测试全部达标才算合格,已知男生甲的50米跑和立定跳远的测试与男生乙的50米跑测试已达标,男生甲还需要参加一分钟的引体向上测试,男生乙还需要参加立定跳远和一分钟引体向上两项测试,若甲参加一分钟引体向上测试达标的概率为p,乙参加立定跳远和一分钟引体向上的测试达标的概率均为 ![]() ,甲乙每一项测试是否达标互不影响,已知甲和乙同时合格的概率为
,甲乙每一项测试是否达标互不影响,已知甲和乙同时合格的概率为 ![]() .
.
(1)求p的值,并计算甲和乙恰有一人合格的概率;
(2)在三项测试项目中,设甲达标的测试项目项数为x,乙达标的测试项目项数为y,记ξ=x+y,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】规定记号“*”表示一种运算,a*b=a2+ab,设函数f(x)=x*2,且关于x的方程f(x)=ln|x+1|(x≠﹣1)恰有4个互不相等的实数根x1 , x2 , x3 , x4 , 则x1+x2+x3+x4= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 是奇函数,g(x)=log2(2x+1)-bx是偶函数.
是奇函数,g(x)=log2(2x+1)-bx是偶函数.
(1)求a-b;
(2)若对任意的t∈[-1,2],不等式f(t2-2t-1)+f(2t2-k)<0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(0<b<3)的左右焦点分别为E,F,过点F作直线交椭圆C于A,B两点,若
=1(0<b<3)的左右焦点分别为E,F,过点F作直线交椭圆C于A,B两点,若 ![]() 且
且 ![]()

(1)求椭圆C的方程;
(2)已知点O为原点,圆D:(x﹣3)2+y2=r2(r>0)与椭圆C交于M,N两点,点P为椭圆C上一动点,若直线PM,PN与x轴分别交于点R,S,求证:|OR||OS|为常数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com