
【题目】点![]() 与定点
与定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离的比是常数
的距离的比是常数![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过坐标原点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() ,
,![]() 两点,轨迹
两点,轨迹![]() 上异于
上异于![]() ,
,![]() 的点
的点![]() 满足直线
满足直线![]() 的斜率为
的斜率为![]() .
.
(ⅰ)求直线![]() 的斜率;
的斜率;
(ⅱ)求![]() 面积的最大值.
面积的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,极点为![]() ,一条封闭的曲线
,一条封闭的曲线![]() 由四段曲线组成:
由四段曲线组成:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求该封闭曲线所围成的图形面积;
(2)若直线![]() :
:![]() 与曲线
与曲线![]() 恰有3个公共点,求
恰有3个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】音乐与数学有着密切的联系,我国春秋时期有个著名的“三分损益法”:以“宫”为基本音,“宫”经过一次“损”,频率变为原来的![]() ,得到“徵”;“徵”经过一次“益”,频率变为原来的
,得到“徵”;“徵”经过一次“益”,频率变为原来的![]() ,得到“商”;…….依次损益交替变化,获得了“宫、徵、商、羽、角”五个音阶.据此可推得( )
,得到“商”;…….依次损益交替变化,获得了“宫、徵、商、羽、角”五个音阶.据此可推得( )
A.“宫、商、角”的频率成等比数列B.“宫、徵、商”的频率成等比数列
C.“商、羽、角”的频率成等比数列D.“徵、商、羽”的频率成等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() 、
、![]() (不与左右顶点重合),连结
(不与左右顶点重合),连结![]() 、
、![]() ,已知
,已知![]() 周长为8.
周长为8.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率为1,求
的斜率为1,求![]() 的面积;
的面积;
(3)设![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信运动,是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注微信运动公众号查看自己每天或每月行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
根据折线图,下列结论正确的是( )
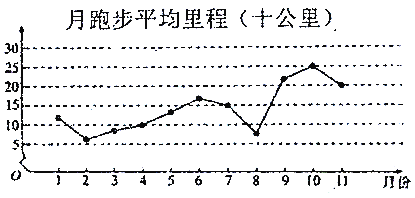
A. 月跑步平均里程的中位数为![]() 月份对应的里程数
月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在![]() 、
、![]() 月
月
D. ![]() 月至
月至![]() 月的月跑步平均里程相对于
月的月跑步平均里程相对于![]() 月至
月至![]() 月,波动性更小,变化比较平稳
月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆![]() 过点
过点![]() ,
,![]() ,
,![]() 是两个焦点.以椭圆
是两个焦点.以椭圆![]() 的上顶点
的上顶点![]() 为圆心作半径为
为圆心作半径为![]() 的圆,
的圆,
(1)求椭圆![]() 的方程;
的方程;
(2)存在过原点的直线![]() ,与圆
,与圆![]() 分别交于
分别交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点(点
两点(点![]() 在线段
在线段![]() 上),使得
上),使得![]() ,求圆
,求圆![]() 半径
半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com