
 ��ijУ��֯�ġ������й��Ρ�������У��ס����������6λѡ�ֲ������ڵ�һ�ֱ��Ի����У���ί�����ǵı��Գɼ���Ϊ�������ݣ����Ƴ���ͼ��ʾ�ľ�Ҷͼ��Ϊ�����ӽ�������ظУ���������ʱû�й����ס����������һλѡ�ֵijɼ���
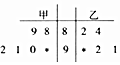
��ijУ��֯�ġ������й��Ρ�������У��ס����������6λѡ�ֲ������ڵ�һ�ֱ��Ի����У���ί�����ǵı��Գɼ���Ϊ�������ݣ����Ƴ���ͼ��ʾ�ľ�Ҷͼ��Ϊ�����ӽ�������ظУ���������ʱû�й����ס����������һλѡ�ֵijɼ������� �����ȷֱ�����װ�ǰ5λѡ�ֵ��ֺܷ��Ұ�ǰ5λѡ�ֵ��ܷ֣��ɴ������оٷ�������Ұ��ֳܷ����װ�ĸ��ʣ�
���ֱ�����ס��������ƽ���֡�����ɴ�����������
��� �⣺���װ�ǰ5λѡ�ֵ��ܷ�Ϊ��88+89+90+91+92=450��
�Ұ�ǰ5λѡ�ֵ��ܷ�Ϊ��82+84+92+91+94=443��
���Ұ��ֳܷ����װ࣬��ס����������λѡ�ֵijɼ��ɷֱ�Ϊ��
��90��98������90��99������91��99�����������
���Ұ��ֳܷ����װ�ĸ���p=$\frac{3}{10��10}$=$\frac{3}{100}$��
���װ�ƽ����Ϊ$\overline{{x}_{��}}$=$\frac{1}{6}$��88+89+90+91+92+90��=90��
�Ұ�ƽ����Ϊ$\overline{{x}_{��}}$=$\frac{1}{6}$��82+84+92+91+94+97��=90��
�װ��S2��=$\frac{1}{6}$��22+12+12+22��=$\frac{5}{3}$��
�Ұ��S2��=$\frac{1}{6}$��82+62+22+12+42+72��=$\frac{85}{3}$��
�����ƽ������ͬ�����װ�ѡ�ֵķ���С���Ұ࣬
��װ�ѡ�ּ��ʵ���൱������
�Ұ�ѡ�ּ�ʵ�����⣬���ϴ�
���� ���⿼�龥Ҷͼ��Ӧ�ã�������ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
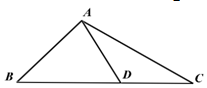 ��ͼ���ڡ�ABC�У���B=45�㣬D��BC����һ�㣬AB=$\frac{5}{2}\sqrt{6}$��AC=5$\sqrt{3}$��AD=5����ADBΪ��ǣ�
��ͼ���ڡ�ABC�У���B=45�㣬D��BC����һ�㣬AB=$\frac{5}{2}\sqrt{6}$��AC=5$\sqrt{3}$��AD=5����ADBΪ��ǣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 2 | C�� | 2$\sqrt{2}$ | D�� | 2$\sqrt{2}$+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����3��0�� | B�� | ��0����3�� | C�� | ����9��0�� | D�� | ��0����9�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��m�ͦ���m��n����n�Φ� | B�� | ��m�Φ���n�Φ�����m��n | ||
| C�� | ��m?�£��Ҧ��ͦ£���m�ͦ� | D�� | ��m�ͦ£��Ҧ��Φ£���m�ͦ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-3��2] | B�� | [-3��2�� | C�� | ��-3��2�� | D�� | ��-3��2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{x}^{2}}{4}$-y2=1 | B�� | $\frac{{x}^{2}}{2}$-y2=1 | C�� | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{3}$=1 | D�� | x2-3y2=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x+y-4=0 | B�� | 2x+y+4=0 | C�� | x-2y+3=0 | D�� | x-2y-3=0 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com