
【题目】已知函数f(x)=ex﹣ln(x+a)(a∈R)有唯一的零点x0 , 则( )
A.﹣1<x0<﹣ ![]()
B.﹣ ![]() <x0<﹣
<x0<﹣ ![]()
C.﹣ ![]() <x0<0
<x0<0
D.0<x0< ![]()
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP=4,AB=BC=2,M为PC的中点. 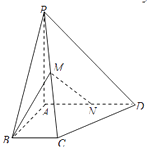
(1)求异面直线AP,BM所成角的余弦值;
(2)点N在线段AD上,且AN=λ,若直线MN与平面PBC所成角的正弦值为 ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}中,其前n项和为Sn , 且 ![]() ,等比数列{bn}中,其前n项和为Tn , 且
,等比数列{bn}中,其前n项和为Tn , 且 ![]() ,(n∈N*)
,(n∈N*)
(1)求an , bn;
(2)求{anbn}的前n项和Mn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线l的参数方程为 ![]() (t为参数,0<α<π),曲线C的极坐标方程为ρsin2θ=4cosθ. (Ⅰ)求曲线C的直角坐标方程;
(t为参数,0<α<π),曲线C的极坐标方程为ρsin2θ=4cosθ. (Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于A、B两点,当α变化时,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P( ![]() ,
, ![]() )在椭圆E:
)在椭圆E: ![]() +
+ ![]() =1(a>b>0)上,F为右焦点,PF垂直于x轴,A,B,C,D为椭圆上四个动点,且AC,BD交于原点O.
=1(a>b>0)上,F为右焦点,PF垂直于x轴,A,B,C,D为椭圆上四个动点,且AC,BD交于原点O.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设A(x1 , y1),B(x2 , y2),满足 ![]() =
= ![]() ,判断kAB+kBC的值是否为定值,若是,求出此定值,并求出四边形ABCD面积的最大值,否则请说明理由.
,判断kAB+kBC的值是否为定值,若是,求出此定值,并求出四边形ABCD面积的最大值,否则请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8. 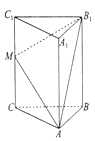
(1)求证:平面AB1M⊥平面A1ABB1;
(2)求平面AB1M与平面ABC所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,曲线C的参数方程为 ![]() (t为参数,a>0)以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,已知直线l的极坐标方程为
(t为参数,a>0)以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,已知直线l的极坐标方程为 ![]() . (Ⅰ)设P是曲线C上的一个动点,当a=2时,求点P到直线l的距离的最小值;
. (Ⅰ)设P是曲线C上的一个动点,当a=2时,求点P到直线l的距离的最小值;
(Ⅱ)若曲线C上的所有点均在直线l的右下方,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学上称函数y=kx+b(k,b∈R,k≠0)为线性函数.对于非线性可导函数f(x),在点x0附近一点x的函数值f(x),可以用如下方法求其近似代替值:f(x)≈f(x0)+f'(x0)(x﹣x0).利用这一方法, ![]() 的近似代替值( )
的近似代替值( )
A.大于m
B.小于m
C.等于m
D.与m的大小关系无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com