
【题目】已知函数![]() ,
,![]()
![]() .
.
(1)求函数![]() 的单调区间与极值.
的单调区间与极值.
(2)当![]() 时,是否存在
时,是否存在![]() ,使得
,使得![]() 成立?若存在,求实数
成立?若存在,求实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
【答案】(1)分类讨论,详见解析;(2)![]() .
.
【解析】
(1)求出函数![]() 的定义域,接着求导,对参数
的定义域,接着求导,对参数![]() 分类讨论。
分类讨论。
(2)假设存在![]() ,使得
,使得![]() 成立,则对
成立,则对![]() ,满足
,满足![]() ,将问题转化为求
,将问题转化为求![]() 与
与![]() 。
。
解:(1)![]() ,
,
当![]() 时,
时,![]() 恒成立,即函数
恒成立,即函数![]() 的单调增区间为
的单调增区间为![]() ,无单调减区间,所以不存在极值.
,无单调减区间,所以不存在极值.
当![]() 时,令
时,令![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
故函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ,此时函数
,此时函数![]() 在
在![]() 处取得极大值,极大值为
处取得极大值,极大值为
综上,当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() ,无单调减区间,不存在极值.当
,无单调减区间,不存在极值.当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ,极大值为
,极大值为![]() ,无极小值
,无极小值
(2)当![]() 时,假设存在
时,假设存在![]() ,使得
,使得![]() 成立,则对
成立,则对![]() ,满足
,满足![]()
由![]()
![]() 可得,
可得,
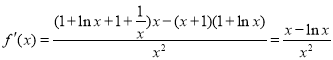 .
.
令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]()
由(1)可知,①当![]() 时,即
时,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 的最小值是
的最小值是![]() .
.
②当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 的最小值是
的最小值是![]() .
.
③当![]() 时,即
时,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.又
上单调递减.又![]() ,所以当
,所以当![]() 时,
时,![]() 在
在![]() 上的最小值是
上的最小值是![]() .当
.当![]() 时,
时,![]() 在
在![]() 上的最小值是
上的最小值是![]()
所以当![]() 时,
时,![]() 在
在![]() 上的最小值是
上的最小值是![]() ,故
,故![]() ,
,
解得![]() ,所以
,所以![]() .
.
当![]() 时,函数
时,函数![]() 在
在![]() 上的最小值是
上的最小值是![]() ,故
,故![]() ,
,
解得![]() ,所以
,所以![]() .故实数
.故实数![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】西北某省会城市计划新修一座城市运动公园,设计平面如图所示:其为五边形![]() ,其中三角形区域
,其中三角形区域![]() 为球类活动场所;四边形
为球类活动场所;四边形![]() 为文艺活动场所,
为文艺活动场所,![]() ,为运动小道(不考虑宽度)
,为运动小道(不考虑宽度)![]() ,
,![]() ,
,![]() 千米.
千米.

(1)求小道![]() 的长度;
的长度;
(2)求球类活动场所![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年是中国改革开放的第40周年,为了充分认识新形势下改革开放的时代性,某地的民调机构随机选取了该地的100名市民进行调查,将他们的年龄分成6段:![]() ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.

(1)现从年龄在![]() 内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用
内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用![]() 表示年龄在
表示年龄在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若用样本的频率代替概率,用随机抽样的方法从该地抽取20名市民进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() .当
.当![]() 最大时,求
最大时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用一张长为12,宽为8的铁皮围成圆柱形的侧面,则这个圆柱的体积为_____;半径为R的半圆形铁皮卷成一个圆锥筒,那么这个圆锥筒的高是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】回答下列两个问题, 并给出例子或证明.
(1)对任意正整数![]() , 在平面上是否都存在
, 在平面上是否都存在![]() 个不在同一条直线上的点, 使得任意两点间的距离都为正整数?
个不在同一条直线上的点, 使得任意两点间的距离都为正整数?
(2)在平面上是否存在两两不同的无限点列组成的点集![]() , 使得
, 使得![]() 内所有点不在同一条直线上, 且
内所有点不在同一条直线上, 且![]() 内任意两点间的距离为正整数?
内任意两点间的距离为正整数?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com