【题目】如图中有一个信号源和五个接收器．接收器与信号源在同一个串联线路中时，就能接收到信号，否则就不能接收到信号．若将图中左端的六个接线点随机地平均分成三组，将右端的六个接线点也随机地平均分成三组，再把所得六组中每组的两个接线点用导线连接，则这五个接收器能同时接收到信号的概率是（ ）．
A.
B.
C.
D.
【答案】D
【解析】
先将左端的六个接线点随机地平均分成三组可能出现的所有结果找出来，再根据五个接收器能同时接收到信号必须全部在同一个串联线路中，求出此种情况可能出现的结果，再运用古典概型的概率公式即可得出所求事件概率．
解：根据题意，设右端连线方式如图，
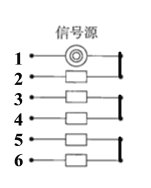
对于左端的六个接线点，将其随机地平均分成三组，共有
种结果，
五个接收器能同时接收到信号必须全部在同一个串联线路中，则1必须和3、4、5、6中其中1个相接，接好后，2只有2种情况可选，剩下的接线点只有1种接法，所以共有
种结果，
同理，右端连线方式变化时，左端的接线方法都有15种，其中有8种可以收到信号，
∴这五个接收器能同时接收到信号的概率是
，
故选：D．
科目：高中数学 来源： 题型：
【题目】已知三棱柱
中，
，
，点
为
的中点，
.
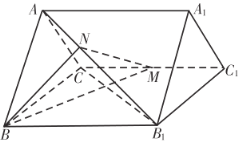
（1）求证：
平面
；
（2）条件①：直线
与平面
所成的角为
；
条件②：
为锐角，三棱锥
的体积为
.
在以上两个条件中任选一个，补充在下面的问题中，并解决该问题：
若平面
平面，______，求平面与平面所成的锐二面角的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，曲线C的参数方程为
（
为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为
.
（1）求曲线C的极坐标方程和直线l的直角坐标方程；
（2）若射线
与曲线C交于点A（不同于极点O），与直线l交于点B，求
的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某单位一辆交通车载有8个职工从单位出发送他们下班回家，途中共有甲、乙、丙3个停车点．如果某停车点无人下车，那么该车在这个点就不停车．假设每个职工在每个停车点下车的可能性都是相等的，求下列事件的概率：
（1）该车在某停车点停车；
（2）停车的次数不少于2次；
（3）恰好停车2次．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如果执行程序框图，输入正整数
，
，满足
，那么输出的
等于（ ）．
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/25/2492401463009280/2492946029182977/STEM/3a3c20c7c34c41528daf48813411739a.png]
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，正四棱锥
底面的四个顶点
，
，
，
在球
的同一个大圆上，点
在球面上，且已知
．
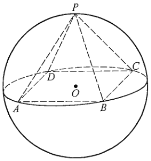
（1）求球的表面积；
（2）设
为
中点，求异面直线
与
所成角的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD与△ACD折成互相垂直的两个平面后，某学生得出下列四个结论：
①
；
②∠BAC＝60°；
③三棱锥D﹣ABC是正三棱锥；
④平面ADC的法向量和平面ABC的法向量互相垂直．
其中正确结论的序号是 ．（请把正确结论的序号都填上）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
