
【题目】已知函数f(x)=lnx﹣a(x﹣1),g(x)=ex .
(1)当a=2时,求函数f(x)的最值;
(2)当a≠0时,过原点分别作曲线y=f(x)与y=g(x)的切线l1 , l2 , 已知两切线的斜率互为倒数,证明: ![]() <a<
<a< ![]() .
.
【答案】
(1)解:当a=2时,f(x)=lnx﹣2(x﹣1)的定义域为(0,+∞),
f′(x)= ![]() ﹣2=
﹣2= ![]() ;
;
当x∈(0, ![]() )时,f′(x)>0,当x∈(
)时,f′(x)>0,当x∈( ![]() ,+∞)时,f′(x)<0,
,+∞)时,f′(x)<0,
即函数f(x)在(0, ![]() )上单调递增,在(
)上单调递增,在( ![]() ,+∞)上单调递减.
,+∞)上单调递减.
所以f(x)max=f( ![]() )=1﹣ln2,没有最小值
)=1﹣ln2,没有最小值
(2)解:证明:设切线l2的方程为y=k2x,切点为(x2,y2),则y2= ![]() ,
,
k2=g′(x2)= ![]() =
= ![]() ,
,
所以x2=1,y2=e,则k2=e.
由题意知,切线l1的斜率为k1= ![]() =
= ![]() ,l1的方程为y=
,l1的方程为y= ![]() x;
x;
设l1与曲线y=f(x)的切点为(x1,y1),则k1=f′(x1)= ![]() ﹣a=
﹣a= ![]() =
= ![]() ,
,
所以y1= ![]() =1﹣ax1,a=
=1﹣ax1,a= ![]() ﹣
﹣ ![]() .
.
又因为y1=lnx1﹣a(x1﹣1),消去y1和a后,
整理得lnx1﹣1+ ![]() ﹣
﹣ ![]() =0.
=0.
令m(x)=lnx﹣1+ ![]() ﹣
﹣ ![]() =0,
=0,
则m′(x)= ![]() ﹣
﹣ ![]() =
= ![]() ,m(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
,m(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
若x1∈(0,1),因为m( ![]() )=﹣2+e﹣
)=﹣2+e﹣ ![]() >0,m(1)=﹣
>0,m(1)=﹣ ![]() <0,所以x1∈(
<0,所以x1∈( ![]() ,1),
,1),
而a= ![]() ﹣
﹣ ![]() 在x1∈(
在x1∈( ![]() ,1)上单调递减,所以
,1)上单调递减,所以 ![]() <a<
<a< ![]() .
.
若x1∈(1,+∞),因为m(x)在(1,+∞)上单调递增,且m(e)=0,则x1=e,
所以a= ![]() ﹣
﹣ ![]() =0(舍去).
=0(舍去).
综上可知, ![]() <a<
<a< ![]()
【解析】(1)当a=2时,f(x)=lnx﹣2(x﹣1)的定义域为(0,+∞),再利用导数求函数的单调区间,从而求解函数的最值;(2)设切线l2的方程为y=k2x,从而由导数及斜率公式可求得切点为(1,e),k2=e;再设l1的方程为y= ![]() x;设l1与曲线y=f(x)的切点为(x1 , y1),从而可得y1=
x;设l1与曲线y=f(x)的切点为(x1 , y1),从而可得y1= ![]() =1﹣ax1 , a=
=1﹣ax1 , a= ![]() ﹣
﹣ ![]() ;结合y1=lnx1﹣a(x1﹣1)可得lnx1﹣1+
;结合y1=lnx1﹣a(x1﹣1)可得lnx1﹣1+ ![]() ﹣
﹣ ![]() =0,再令m(x)=lnx﹣1+
=0,再令m(x)=lnx﹣1+ ![]() ﹣
﹣ ![]() ,从而求导确定函数的单调性,从而确定
,从而求导确定函数的单调性,从而确定 ![]() <a<
<a< ![]() ,问题得证.
,问题得证.
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】甲,乙两人进行围棋比赛,共比赛2n(n∈N+)局,根据以往比赛胜负的情况知道,每局甲胜的概率和乙胜的概率均为 ![]() .如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
.如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
(1)求P(2)与P(3)的值;
(2)试比较P(n)与P(n+1)的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,以原点O为顶点,以y轴为对称轴的抛物线E的焦点为F(0,1),点M是直线l:y=m(m<0)上任意一点,过点M引抛物线E的两条切线分别交x轴于点S,T,切点分别为B,A.
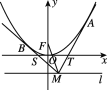
(1)求抛物线E的方程;
(2)求证:点S,T在以FM为直径的圆上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的四棱锥P﹣ABCD中,四边形ABCD为正方形,PA⊥CD,BC⊥平面PAB,且E,M,N分别为PD,CD,AD的中点, ![]() =3
=3 ![]() .
. 
(1)证明:PB∥平面FMN;
(2)若PA=AB,求二面角E﹣AC﹣B的余弦值. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A,B,C的对边分别是a,b,c,3sin2C+8sin2A=11sinAsinC,且c<2a.
(1)求证:△ABC为等腰三角形
(2)若△ABC的面积为8 ![]() .且sinB=
.且sinB= ![]() ,求BC边上的中线长.
,求BC边上的中线长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() =1(a>b>0)的左、右顶点分别为A,B,焦距为2
=1(a>b>0)的左、右顶点分别为A,B,焦距为2 ![]() ,直线x=﹣a与y=b交于点D,且|BD|=3
,直线x=﹣a与y=b交于点D,且|BD|=3 ![]() ,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P.
,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P. 
(1)求椭圆的方程;
(2)证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法中,
①命题“存在x∈R,x2﹣x>0”的否定是“对于任意x∈R,x2﹣x<0”;
②命题“p且q为真”是“p或q为真”的必要不充分条件;
③已知幂函数f(x)=xα的图象经过点(2, ![]() ),则f(4)的值等于
),则f(4)的值等于 ![]() ;
;
④已知向量 ![]() =(3,﹣4),
=(3,﹣4), ![]() =(2,1),则向量
=(2,1),则向量 ![]() 在向量
在向量 ![]() 方向上的投影是
方向上的投影是 ![]() .
.
说法错误的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图4所示,其中成绩分组区间是: ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示,求数学成绩在
之比如下表所示,求数学成绩在![]() 之外的人数.
之外的人数.
分数段 |
|
|
|
|
X:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com