
(本题满分14分)已知函数f(x)满足2ax·f(x)=2f(x)-1,f(1)=1,设无穷数列{an}满足an+1=f(an).(1)求函数f(x)的表达式;(2)若a1=3,从第几项起,数列{an}中的项满足an<an+1;(3)若![]() <a1<
<a1<![]() (m为常数且m∈N+,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立。
(m为常数且m∈N+,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立。
(1)![]()
(1)当a=0时,有0=2f(x)-1,把f(1)=1代入2f(x)-1=1≠0,则a≠0,当a≠0时,f(x)=-![]() ,
,
又f(1)=1![]()
![]() , ∴
, ∴![]() , 4 分
, 4 分
(2)若a1=3,由![]()
![]() ,
,![]() ,
,
假设当n≥3时,0<an<1,则0<an+1=![]() <
<![]() =1
=1![]() 2-an>0,从而an+1-an=
2-an>0,从而an+1-an=![]() >0
>0 ![]() an+1>an 从第2项起,数列{an}中的项满足an<an+1 9分
an+1>an 从第2项起,数列{an}中的项满足an<an+1 9分
另解:由![]()
![]()
![]()
∴要满足an<an+1,即![]() <
<![]() ,
, ![]() <0
<0![]() >0
>0![]() n>
n>![]() 或n<
或n<![]() ,又∵n∈N*,∴n>
,又∵n∈N*,∴n>![]() ,∴从第2项起,数列{an}中的项满足an<an+1 9分
,∴从第2项起,数列{an}中的项满足an<an+1 9分
(3)当![]() <a1<
<a1<![]() 时,由
时,由![]() <a2<
<a2<![]() ,同理
,同理![]() <a3<
<a3<![]() ,假设
,假设![]() <an<
<an<![]() ,由
,由![]() 与归纳假设知
与归纳假设知![]() <am,即am>2
<am,即am>2
∴![]() <0,0<am+2=
<0,0<am+2=![]() <
<![]() =1 ∴N=m+2,使得当n≥N时,总有0<an<1 14分
=1 ∴N=m+2,使得当n≥N时,总有0<an<1 14分
另解:由(2)的方法2可得 ![]()
要使0<an<1,则0<![]() <1
<1![]() -1<
-1<![]() <1
<1![]() -1<
-1<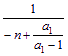 <0
<0![]()
即当![]() <n-2时,总有0<an<1,又∵
<n-2时,总有0<an<1,又∵![]() <a1<
<a1<![]() <m-1<
<m-1<![]() <m
<m
∴m≤n-2![]() n≥m+2 ∴当N=m+2,使得当n≥N时总有0<an<1 14分
n≥m+2 ∴当N=m+2,使得当n≥N时总有0<an<1 14分


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源:2012-2013学年吉林省高三第一次月考文科数学试卷(解析版) 题型:解答题
(本题满分14分)已知函数
(1)若 ,求x的值;
,求x的值;
(2)若 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省惠州市高三第三次调研考试数学理卷 题型:解答题
(本题满分14分)
已知椭圆 :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 相交于
相交于 、
、 ,
, .
.
⑴求 、
、 的值;
的值;
⑵若动圆 与椭圆
与椭圆 和直线
和直线 都没有公共点,试求
都没有公共点,试求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省惠州市高三第三次调研考试数学理卷 题型:解答题
((本题满分14分)
已知梯形ABCD中,AD∥BC,∠ABC =∠BAD = ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
(1)当x=2时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为 ,
,
求 的最大值;
的最大值;


(3)当 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com