
【题目】如图,四棱锥PABCD中,侧面PAD是正三角形,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.
(1)求证:PC⊥AD.
(2)在棱PB上是否存在一点Q,使得A,Q,M,D四点共面?若存在,指出点Q的位置并证明;若不存在,请说明理由.

【答案】(1)见解析;(2)见解析
【解析】
(1)取AD的中点O,连接OP,OC,AC,由线面垂直判定定理证明AD⊥平面POC,继而得到PC⊥AD
(2)取棱PB的中点Q,连接QM,证明QM∥AD,从而A,Q,M,D四点共面
(1)证明:如图,取AD的中点O,连接OP,OC,AC.
依题意可知△PAD,△ACD均为正三角形.
所以OC⊥AD,OP⊥AD.
又OC∩OP=O,OC平面POC,OP平面POC,所以AD⊥平面POC.
又PC平面POC,所以PC⊥AD.
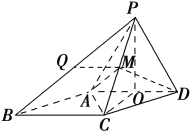
(2)解:当点Q为棱PB的中点时,A,Q,M,D四点共面.
证明如下:
取棱PB的中点Q,连接QM.
因为M为PC的中点,所以QM∥BC.
在菱形ABCD中,AD∥BC,所以QM∥AD.
所以A,Q,M,D四点共面.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】 设命题p:函数y=![]() 在定义域上为减函数;命题q:a,b∈(0,+∞),当a+b=1时,
在定义域上为减函数;命题q:a,b∈(0,+∞),当a+b=1时,![]() +
+![]() =3.以下说法正确的是( )
=3.以下说法正确的是( )
A. p∨q为真B. p∧q为真
C. p真q假D. p,q均假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCDA1B1C1D1中,M,N分别是棱AB,CC1的中点,△MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:

①平面MB1P⊥ND1;
②平面MB1P⊥平面ND1A1;
③△MB1P在底面ABCD上的射影图形的面积为定值;
④△MB1P在侧面DD1C1C上的射影图形是三角形.
其中正确的命题序号是( )
A. ①B. ②③
C. ①③D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知AB为圆O的直径,且AB=4,点D为线段AB上一点,且![]() ,点C为圆O上一点,且
,点C为圆O上一点,且![]() .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.
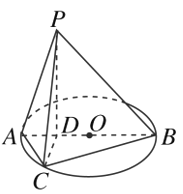
(1)求证:CD⊥平面PAB;
(2)求直线PC与平面PAB所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知函数![]()
(1)若直线![]() 过点
过点![]() ,并且与曲线
,并且与曲线![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)设函数![]() 在
在![]() 上有且只有一个零点,求
上有且只有一个零点,求![]() 的取值范围。(其中
的取值范围。(其中![]() 为自然对数的底数)
为自然对数的底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com