
 的左右焦点分别为F1、F2,动点P满足|PF1|+|PF2|>6,则动点P不一定在该椭圆外部;
的左右焦点分别为F1、F2,动点P满足|PF1|+|PF2|>6,则动点P不一定在该椭圆外部;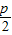 为半径的圆与该抛物线必有3个不同的公共点;
为半径的圆与该抛物线必有3个不同的公共点; 与椭圆
与椭圆 有相同的焦点;
有相同的焦点; 为半径的圆的方程为
为半径的圆的方程为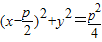 ,与抛物线y2=2px联立,即可求得交点的个数;
,与抛物线y2=2px联立,即可求得交点的个数; 的左右焦点分别为F1、F2,∴椭圆上的点P′满足|P′F1|+|P′F2|=10,∴动点P满足|PF1|+|PF2|>6,则动点P不一定在该椭圆外部,故①为真命题;
的左右焦点分别为F1、F2,∴椭圆上的点P′满足|P′F1|+|P′F2|=10,∴动点P满足|PF1|+|PF2|>6,则动点P不一定在该椭圆外部,故①为真命题; 为半径的圆的方程为
为半径的圆的方程为 ,将抛物线y2=2px代入,并化简可得:x2+px=0,∵x≥0,p>0,∴x=0,∴以抛物线y2=2px(p>0)的焦点为圆心,以
,将抛物线y2=2px代入,并化简可得:x2+px=0,∵x≥0,p>0,∴x=0,∴以抛物线y2=2px(p>0)的焦点为圆心,以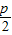 为半径的圆与该抛物线有1个公共点,故②为假命题;
为半径的圆与该抛物线有1个公共点,故②为假命题; 的焦点为(
的焦点为( ,0),椭圆
,0),椭圆 的焦点为(
的焦点为( ,0),因此双曲线
,0),因此双曲线 与椭圆
与椭圆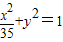 有相同的焦点,故③为真命题;
有相同的焦点,故③为真命题; =
=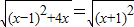


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| x2 |
| 25 |
| y2 |
| 16 |
| p |
| 2 |
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
查看答案和解析>>
科目:高中数学 来源:2010年黑龙江省高二上学期期中考试文科数学卷 题型:填空题
给出下列命题:
①若椭圆长轴长与短轴长的和为 ,焦距为
,焦距为 ,则椭圆的标准方程为
,则椭圆的标准方程为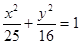 ;
;
②曲线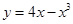 在点
在点 处的切线方程是
处的切线方程是 ;
;
③命题“若 ,则
,则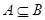 ”的逆否命题是:“若
”的逆否命题是:“若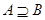 ,则
,则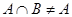 ”;
”;
④高台跳水运动员在 秒时距水面高度
秒时距水面高度 (单位:米),则该运动员的初速度为
(单位:米),则该运动员的初速度为 (米/秒);
(米/秒);
⑤“ ”是“
”是“ ”的充分条件。
”的充分条件。
正确的命题是 。
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列命题:
①若![]() ,
,![]() ,则
,则![]() 的元素有 0个或1个或2个;
的元素有 0个或1个或2个;
②![]() 、
、![]() 是椭圆
是椭圆![]() :
:![]() 的焦点,在
的焦点,在![]() 上使
上使![]() 为直角三角形的点
为直角三角形的点![]() 的个数为8;
的个数为8;
③经过点(1,2)且在两坐标轴上的截距相等的直线l的方程为![]() ;
;
④以椭圆![]() 内的一点
内的一点![]() 为中点的弦所在的直线方程是
为中点的弦所在的直线方程是![]() .
.
其中所有正确命题的序号是 (
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列命题:
①若![]() ,
,![]() ,则
,则![]() 的元素有 0个或1个或2个;
的元素有 0个或1个或2个;
②![]() 、
、![]() 是椭圆
是椭圆![]() :
:![]() 的焦点,在
的焦点,在![]() 上使
上使![]() 为直角三角形的点
为直角三角形的点![]() 的个数为4;
的个数为4;
③在椭圆![]() 中,通过点
中,通过点![]() 且被这点平分的弦所在的直线方程是
且被这点平分的弦所在的直线方程是![]() ;
;
④在圆![]() 内,过点
内,过点![]() 有
有![]() 条弦的长度成等差数列,最短弦的长为数列的首项
条弦的长度成等差数列,最短弦的长为数列的首项![]() ,最长弦的长为数列的末项
,最长弦的长为数列的末项![]() ,若公差
,若公差![]() ,则
,则![]() 的取值集合为
的取值集合为![]() ,
,
其中所有正确命题的序号是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com