已知

、

、

是同一平面内的三个向量,其中

(1)若

,且

,求

的坐标;
(2)若

,且

与

垂直,求

与

的夹角

.
(1)(2,4)或(-2,-4);(2)
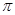
试题分析:(1)由

,可设
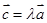
,再利用向量模公式列出关于

的方程,求出

即可写出

的坐标;(2)先算出

的模,由

与

垂直知,

与

数量积为0,利用向量数量积的运算法则,求出

与

的数量积,在利用向量夹角公式求出

与

的夹角.
试题解析:(1)由题设知:
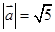
,于是有

2分
由

得
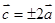
, 4分
∴

或
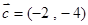
6分
(2)∵
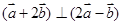
∴

即
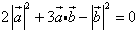
8分
由
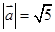
,

知:

10分
∴
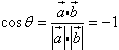
11分
又由

得 :

12分(其他写法参照给分)
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知△
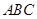
的面积
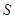
满足
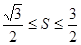
,且
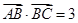
,
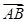
与
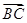
的夹角为
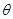
.
(1)求
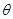
的取值范围;
(2)求函数
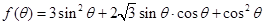
的最大值及最小值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知向量

,

,且

.
(1)求

及

;
(2)若

的最小值为

,求实数

的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
平面内给定三个向量
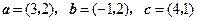
.
(1)求满足
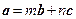
的实数

;
(2)求满足

的实数
k;
(3)设
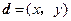
满足
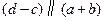
且
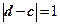
,求
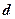
.
查看答案和解析>>

 、
、 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中
 ,且
,且 ,求
,求 的坐标;
的坐标; ,且
,且 与
与 垂直,求
垂直,求 与
与 的夹角
的夹角 .
.