
【题目】(1)如图,以过原点的直线的倾斜角![]() 为参数,求圆
为参数,求圆![]() 的参数方程;
的参数方程;
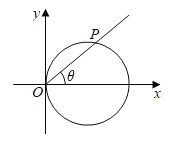
(2)在平面直角坐标系中,已知直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),若
为参数),若![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的长.
的长.
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】贺先生想向银行贷款买辆新能源车,银行可以贷给贺先生N元,一年后需要一次性还1.02N元.
(1)贺先生发现一个投资理财方案:每个月月初投资![]() 元,共投资一年,每月的月收益率达到1%,于是贺先生决定贷款12
元,共投资一年,每月的月收益率达到1%,于是贺先生决定贷款12![]() 元,按投资方案投资,求
元,按投资方案投资,求![]() 的值,使得贺先生用最终投所得的钱还清贷款后,还有120000的余额去旅游(精确到0.01元);
的值,使得贺先生用最终投所得的钱还清贷款后,还有120000的余额去旅游(精确到0.01元);
(2)贺先生又发现一个投资方案:第![]() 个月月初投资
个月月初投资![]() 元
元![]() 共投资一年,每月的月收益率达到1%,则贺先生应贷款多少,使得用最终投资所得的钱还清后,还有120000的余额去旅游(精确到0.01元).
共投资一年,每月的月收益率达到1%,则贺先生应贷款多少,使得用最终投资所得的钱还清后,还有120000的余额去旅游(精确到0.01元).
(参考数据![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,
为自然对数的底数,![]() 。
。
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(Ⅱ)若![]() ,问函数
,问函数![]() 有无极值点?若有,请求出极值点的个数;若没有,请说明理由。
有无极值点?若有,请求出极值点的个数;若没有,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形,如图.
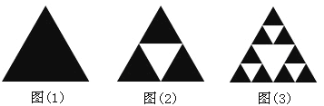
现在上述图(3)中随机选取一个点,则此点取自阴影部分的概率为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)如果函数![]() 的单调递减区间为
的单调递减区间为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(3)若不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果,其中的《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》,有丰富多彩的内容,是了解我国古代数学的重要文献,这5部专著中有3部产生于汉、魏、晋、南北朝时期,某中学拟从这5部专著中选择2部作为“数学文化”校本课程学习内容,则所选2部专著中至少有一部是汉、魏、晋、南北朝时期专著的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com