C
分析:将圆方程化为的标准方程形式,可得圆心为(2,-1)且半径等于1.利用轴对称的知识,解出(2,-1)关于直线x-y+3=0 的对称点为(-4,5),即可得到对称圆的标准方程,再化成一般方程可得本题答案.
解答:将圆x
2+y
2-4x+2y+4=0化成标准方程,得
(x-2)
2+(y+1)
2=1,表示圆心在(2,-1),半径等于1的圆.
因此,可设对称圆的方程为 (x-a)
2+(y-b)
2=1
可得
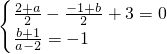
,解之得
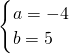
,
即点(2,-1)关于直线x-y+3=0对称的点的坐标为(-4,5),
∴与圆x
2+y
2-4x+2y+4=0关于直线x-y+3=0成轴对称的圆方程是(x+4)
2+(y-5)
2=1,
整理成一般式为:x
2+y
2+8x-10y+40=0
故选:C
点评:本题给出定圆,求该圆关于已知直线对称的圆的方程,着重考查了圆的标准方程和一般方程、直线的对称等知识,属于基础题.

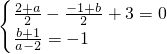 ,解之得
,解之得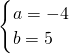 ,
,
