Question

3．如图，在长方形ABCD中，AB=2，AD=1，E为DC的中点，将△DAE沿AE折起，平面DAE⊥平面ABCE，连DB，DC，BE．

（Ⅰ）求证：BE⊥平面ADE；
（Ⅱ）求AC与平面ADE所成角的正弦值．

Answer 1

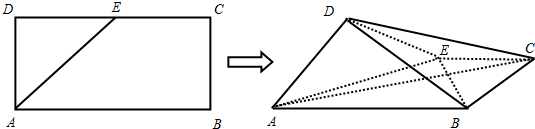
分析 （Ⅰ）在矩形ABCD中，求出AE=BE=$\sqrt{2}$，AB=2，说明AE⊥BE，然后证明BE⊥平面ADE．
（II）由题意BE=$\sqrt{2}$，AC=$\sqrt{5}$，C到平面ADE的距离为$\frac{\sqrt{2}}{2}$，然后求出所成角的正弦值．

解答 （Ⅰ）证明：∵矩形ABCD中，AB=2，AD=1，E为CD的中点．
∴AE=BE=$\sqrt{2}$，AB=2，
∴AE⊥BE，
又∵平面ADE⊥平面ABCE，平面ADE∩平面ABCE=AE，
∴BE⊥平面ADE．…（6分）
（II）解：由题意BE=$\sqrt{2}$，AC=$\sqrt{5}$，C到平面ADE的距离为$\frac{\sqrt{2}}{2}$
AC与平面ADE所成角的正弦值为$\frac{\frac{\sqrt{2}}{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{10}$…（6分）

点评 本题考查直线与平面垂直，折叠问题，直线与平面所成角的求法，考查空间想象能力，计算能力．