
【题目】如图所示,在长方体![]() 中,
中,![]() 为
为![]() 的中点,连接
的中点,连接![]() 和
和![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正切值。
的正切值。
【答案】(1)见解析(2)![]()
【解析】
(1)先由BC⊥平面D1DCC1BC⊥DE.再利用△DD1E为等腰直角三角形∠D1ED=45°以及∠C1EC=45°可得DE⊥EC,合在一起可得平面EDB⊥平面EBC;
(2)先过E在平面D1DCC1中作EO⊥DC于OEO⊥面ABCD;再O在平面DBC中作OF⊥DB于F,利用三垂线定理极其逆定理可得EF⊥BD.所以∠EFO为二面角E-DB-C的平面角.再利用平面几何知识求出∠EFO的正切值即可;
(1)证明:在长方体ABCD-A1B1C1D1中,
AB=2,BB1=BC=1,E为D1C1的中点.
∴△DD1E为等腰直角三角形,∠D1ED=45°.同理∠C1EC=45°.
∴∠DEC=90°,即DE⊥EC.
在长方体ABCD-A1B1C1D1中,BC⊥平面D1DCC1,又DE平面D1DCC1,
∴BC⊥DE.又EC∩BC=C,∴DE⊥平面EBC.
∵DE平面DEB,∵平面DEB⊥平面EBC.
(2)如图,过E在平面D1DCC1中作EO⊥DC于O.
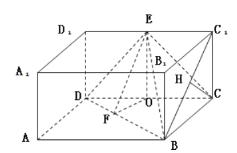
在长方体ABCD-A1B1C1D1中,∵面ABCD⊥面D1DCC1,∴EO⊥面ABCD.
过O在平面DBC中作OF⊥DB于F,
连接EF∴EF⊥BD.
∠EFO为二面角E-DB-C的平面角.
利用平面几何知识可得OF=![]() OE=1,tan∠EFO=
OE=1,tan∠EFO=![]() ,
,
所以二面角E-DB-C的正切值为![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】某大学进行自主招生时,需要进行逻辑思维和阅读表达两项能力的测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如下图所示:


得出下面四个结论:
①甲同学的逻辑排名比乙同学的逻辑排名更靠前
②乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前
③甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前
④甲同学的阅读表达成绩排名比他的逻辑思维成绩排名更靠前
则所有正确结论的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校随机调查80名学生,以研究学生爱好羽毛球运动与性别的关系,得到下面的![]() 列联表:
列联表:
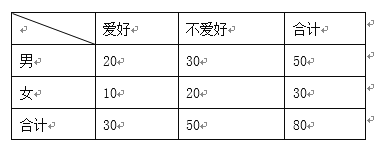
(1)将此样本的频率视为总体的概率,随机调查本校的3名学生,设这3人中爱好羽毛球运动的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)根据表3中数据,能否认为爱好羽毛球运动与性别有关?
附:![]()
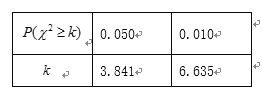
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,
,![]() 表示三条不同的直线,
表示三条不同的直线,![]() ,
,![]() ,
,![]() 表示三个不同的平面,给出下列四个命题:
表示三个不同的平面,给出下列四个命题:
①若![]() ,则
,则![]() ;
;
②若![]() ,
,![]() 是
是![]() 在
在![]() 内的射影,
内的射影,![]()
![]()
![]() ,则
,则![]() ;
;
③若![]() 是平面
是平面![]() 的一条斜线,点
的一条斜线,点![]() ,
,![]() 为过点
为过点![]() 的一条动直线,则可能有
的一条动直线,则可能有![]() 且
且![]() ;
;
④若![]() ,则
,则![]() .
.
其中正确的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的平均数、众数和中位数;
(3)在月平均用电量为,![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在
的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一三棱柱ABC﹣A1B1C1各棱长相等,B1在底面ABC上的射影是AC的中点,则异面直线AA1与BC所成角的余弦值为( )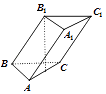
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据(单位:万元):
之间有如下的对应数据(单位:万元):
![]()
(1)求![]() 关于
关于![]() 的线性回归直线方程;
的线性回归直线方程;
(2)据此估计广告费用为10万元时销售收入![]() 的值.
的值.
(附:对于线性回归方程![]() ,其中
,其中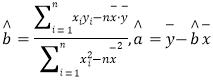 )
)
参考公式: 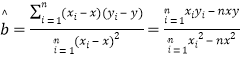
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列. 
(1)求图中实数a的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于80分的人数;
(3)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,记这两名学生成绩在[90,100]内的人数为X,求随机变量X的分布列和期望值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com