
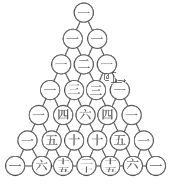
【题目】杨辉三角,又称帕斯卡三角,是二项式系数在三角形中的一种几何排列.在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中用如图所示的三角形解释二项式乘方展开式的系数规律.现把杨辉三角中的数从上到下,从左到右依次排列,得数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1…….记作数列![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】在万众创新的大经济背景下,某成都青年面包店推出一款新面包,每个面包的成本价为![]() 元,售价为
元,售价为![]() 元,该款面包当天只出一炉(一炉至少
元,该款面包当天只出一炉(一炉至少![]() 个,至多
个,至多![]() 个),当天如果没有售完,剩余的面包以每个
个),当天如果没有售完,剩余的面包以每个![]() 元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近
元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近![]() 天的日需求量(单位:个),整理得下表:
天的日需求量(单位:个),整理得下表:
日需求量 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以![]() 天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为
天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为![]() ,记当日这款新面包获得的总利润为
,记当日这款新面包获得的总利润为![]() (单位:元).求
(单位:元).求![]() 的分布列及其数学期望.
的分布列及其数学期望.
相关公式: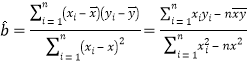 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是双曲线E:
分别是双曲线E: ![]()
![]() 的左、右焦点,P是双曲线上一点,
的左、右焦点,P是双曲线上一点, ![]() 到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当
到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当![]() 时,
时, ![]() 的面积为
的面积为![]() ,求此双曲线的方程。
,求此双曲线的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2-2x-4y=0.
(1)求圆C关于直线x-y-1=0对称的圆D的标准方程;
(2)过点P(4,-4)的直线l被圆C截得的弦长为8,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:①直线![]() 的斜率
的斜率![]() ,则直线
,则直线![]() 的倾斜角
的倾斜角![]() ;②直线
;②直线![]() :
:![]() 与以
与以![]() 、
、![]() 两点为端点的线段相交,则
两点为端点的线段相交,则![]() 或
或![]() ;③如果实数
;③如果实数![]() 满足方程
满足方程![]() ,那么
,那么![]() 的最大值为
的最大值为![]() ;④直线
;④直线![]() 与椭圆
与椭圆![]() 恒有公共点,则
恒有公共点,则![]() 的取值范围是
的取值范围是![]() .其中正确命题的序号是______
.其中正确命题的序号是______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂销售部以箱为单位销售某种零件,每箱的定价为200元,低于100箱按原价销售;不低于100箱通过双方议价,买方能以优惠![]() 成交的概率为0.6,以优惠
成交的概率为0.6,以优惠![]() 成交的概率为0.4.
成交的概率为0.4.
(1)甲、乙两单位都要在该厂购买150箱这种零件,两单位各自达成的成交价相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
(2)某单位需要这种零件650箱,求购买总价![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其中一个焦点F在直线
,其中一个焦点F在直线![]() 上.
上.
(1)求椭圆C的方程;
(2)若直线![]() 和直线
和直线![]() 与椭圆分别相交于点
与椭圆分别相交于点![]() 、
、![]() 、
、![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)若直线![]() 与椭圆交于P,Q两点,试求
与椭圆交于P,Q两点,试求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com