Question

【题目】设函数f（x）=4x3+ ，x∈[0，1]，证明：
（Ⅰ）f（x）≥1﹣2x+3x2；
（Ⅱ） ＜f（x）≤ ．

Answer 1

【答案】证明：（I）令g（x）=（1+x）2（1﹣2x+3x2﹣4x3），x∈[0，1]，

则g′（x）=﹣20（1+x）x3≤0，当且仅当x=0时取等号，

∴g（x）在[0，1]上单调递减，故g（x）≤g（0）=1，

∴（1+x）2（1﹣2x+3x2﹣4x3）≤1，

∴ ≥1﹣2x+3x2，

即f（x）≥1﹣2x+3x2．

（II）由（I）知f（x）≥1﹣2x+3x2=3（x﹣ ）2≥ ，

∵两处等号不能同时成立，

∴f（x）＞ ．

f′（x）=12x2﹣ = ，

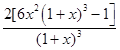令h（x）=6x2（1+x）3﹣1，则f（x）在[0，1]上单调递增，

∵h（0）=﹣1，h（1）=47＞0，

∴h（x）在（0，1）上存在唯一一个零点x0，

∴当0＜x＜x0时，f′（x）＜0，当x0＜x＜1时，f′（x）＞0，

∴f（x）在[0，1]上先减后增，

又f（0）=1，f（1）= ，

∴f（x）≤f（1）= ．

综上， f（x）≤

【解析】（I）构造函数g（x）=（1+x）2（1﹣2x+3x2﹣4x3），判断g（x）的单调性得出最大值，化简即可得出结论；（II）判断f（x）的单调性即可f（x）的最大值，利用（I）得出f（x）＞ ．
【考点精析】本题主要考查了不等式的证明的相关知识点，需要掌握不等式证明的几种常用方法:常用方法有：比较法（作差，作商法）、综合法、分析法；其它方法有：换元法、反证法、放缩法、构造法，函数单调性法，数学归纳法等才能正确解答此题．