
【题目】定义:对于一个项数为![]() 的数列
的数列![]() ,若存在
,若存在![]() 且
且![]() ,使得数列
,使得数列![]() 的前k项和与剩下项的和相等(若仅为1项,则和为该项本身),我们称该数列是“等和数列”.例如:因为
的前k项和与剩下项的和相等(若仅为1项,则和为该项本身),我们称该数列是“等和数列”.例如:因为![]() ,所以数列3,2,1是“等和数列”.请解答以下问题:
,所以数列3,2,1是“等和数列”.请解答以下问题:
(1)数列1,2,p,4是“等和数列”,求实数p的值;
(2)项数为![]() 的等差数列
的等差数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,求证:
,求证:![]() 是“等和数列”.
是“等和数列”.
(3)![]() 是公比为q项数为
是公比为q项数为![]() 的等比数列
的等比数列![]() ,其中
,其中![]() 且
且![]() 恒成立.判断
恒成立.判断![]() 是不是“等和数列”,并证明你的结论.
是不是“等和数列”,并证明你的结论.
【答案】(1)![]() 或
或![]() 或
或![]() (2)证明见解析 (3)
(2)证明见解析 (3)![]() 不是“等和数列”,证明见解析
不是“等和数列”,证明见解析
【解析】
(1)对令![]() 分别计算,得到答案.
分别计算,得到答案.
(2)由![]() ,得
,得![]() ,若
,若![]() 是“等和数列,存在k使得
是“等和数列,存在k使得![]() ,即
,即![]() .分
.分![]() 和
和![]() 进行讨论即可.
进行讨论即可.
(3)假设![]() 是“等和数列”, 则存在
是“等和数列”, 则存在![]() 且
且![]() ,使得
,使得![]() 成立, 即
成立, 即![]() ,
,
由![]() 会得到矛盾,从而判断处结论.
会得到矛盾,从而判断处结论.
(1)若![]() ,即
,即![]() ,则
,则![]() .
.
若![]() ,即
,即![]() ,则
,则![]() .
.
若![]() ,即
,即![]() ,则
,则![]() .
.
所以![]() 或
或![]() 或
或![]()
(2)证明方法一:![]() ,所以
,所以![]() .
.
假设存在k使得数列![]() 的前k项和与剩下项的和相等,即
的前k项和与剩下项的和相等,即![]() ,所以
,所以![]() .
.
![]() ,
,![]() ,
,
即![]() .
.
当![]() 时,
时,![]() ,对任意
,对任意![]() 都有
都有![]() ,
,![]() ,即
,即![]() ,
,
所以此时![]() 是“等和数列”;
是“等和数列”;
当![]() 时,
时,![]() ,
,![]() ,此时
,此时![]() 或
或![]() (舍去).
(舍去).
即存在![]() 且
且![]() ,使得
,使得![]() 成立,所以此时
成立,所以此时![]() 是“等和数列”.
是“等和数列”.
由上得:![]() 是“等和数列”
是“等和数列”
证明方法二:设![]() 公差为d,
公差为d,
![]() ,
,![]() ,
,
同理:![]() ,
,![]() ,
,
于是![]() ,同理
,同理![]() ,
,
![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,
所以![]() ,因为
,因为![]() ,
,
所以![]() ,即存在
,即存在![]() ,使得
,使得![]() ,所以
,所以![]() 是“等和数列”
是“等和数列”
(3)![]() 不是“等和数列”
不是“等和数列”
证明方法一:设![]() 为
为![]() 的前n项和
的前n项和
反证法:假设结论不成立,即![]() 是“等和数列”,
是“等和数列”,
则存在![]() 且
且![]() ,使得
,使得![]() 成立,即
成立,即![]() ,
,
于是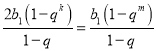 成立,即
成立,即![]()
![]() 时,
时,![]() ,
,![]() ,即
,即![]() ,所以
,所以![]() ,
,
所以![]() ,与
,与![]() 产生矛盾.所以假设不成立,即
产生矛盾.所以假设不成立,即![]() 不是“等和数列”.
不是“等和数列”.
证明方法二:反证法:假设结论不成立,即![]() 是“等和数列”,
是“等和数列”,
则存在![]() 且
且![]() ,使得
,使得![]() 成立,即
成立,即![]() .
.
于是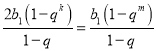 成立,即
成立,即![]() 得到
得到![]() ,
,
这里![]() ,
,![]() 得
得![]() 产生矛盾.所以假设不成立,即
产生矛盾.所以假设不成立,即![]() 不是“等和数列”.
不是“等和数列”.
证明方法三:先证该数列满足:设![]() 为
为![]() 前n项和,则对任意
前n项和,则对任意![]() 都有
都有![]() 成立.
成立.
证明: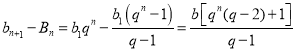 ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
所以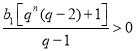 ,所以
,所以![]() 恒成立.
恒成立.
由此得:对任意![]() 且
且![]() ,
,![]() ,即
,即![]() ,
,
所以不存在![]() 且
且![]() ,使得
,使得![]() 成立,
成立,
即![]() 不是“等和数列”.
不是“等和数列”.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为![]() ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生![]() 之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国历法中将一年分为春、夏、秋、冬四个季节,每个季节有六个节气,如夏季包含立夏、小满、芒种、夏至、小暑以及大暑.某美术学院甲、乙、丙、丁四位同学接到绘制二十四节气的彩绘任务,现四位同学抽签确定各自完成哪个季节中的六幅彩绘,在制签及抽签公平的前提下,甲没有抽到绘制春季六幅彩绘任务且乙没有抽到绘制夏季六幅彩绘任务的概率为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,椭圆
中,椭圆![]() 的上焦点为
的上焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点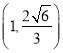 .
.
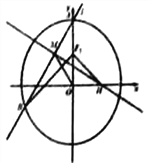
(1)求椭圆![]() 的方程.
的方程.
(2)设过椭圆![]() 的上顶点
的上顶点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】向量集合![]() ,对于任意
,对于任意![]() ,以及任意
,以及任意![]() ,都有
,都有![]() ,则称
,则称![]() 为“
为“![]() 类集”,现有四个命题:
类集”,现有四个命题:
①若![]() 为“
为“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
②若![]() ,
,![]() 都是“
都是“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
③若![]() 都是“
都是“![]() 类集”,则
类集”,则![]() 也是“
也是“![]() 类集”;
类集”;
④若![]() 都是“
都是“![]() 类集”,且交集非空,则
类集”,且交集非空,则![]() 也是“
也是“![]() 类集”.
类集”.
其中正确的命题有________(填所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岸线![]() 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段
一侧有一休闲游乐场,游乐场的前一部分边界为曲线段![]() ,该曲线段是函数
,该曲线段是函数![]() ,
,![]() 的图象,图象的最高点为
的图象,图象的最高点为![]() .边界的中间部分为长1千米的直线段
.边界的中间部分为长1千米的直线段![]() ,且
,且![]() .游乐场的后部分边界是以
.游乐场的后部分边界是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.
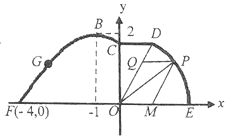
(1)求曲线段![]() 的函数表达式;
的函数表达式;
(2)如图,在扇形![]() 区域内建一个平行四边形休闲区
区域内建一个平行四边形休闲区![]() ,平行四边形的一边在海岸线
,平行四边形的一边在海岸线![]() 上,一边在半径
上,一边在半径![]() 上,另外一个顶点
上,另外一个顶点![]() 在圆弧
在圆弧![]() 上,且
上,且![]() ,求平行四边形休闲区
,求平行四边形休闲区![]() 面积的最大值及此时
面积的最大值及此时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com