练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知不等式（ax+2）ln（x+a）≤0对x∈（﹣a，+∞）恒成立，则a的值为 ．

    【答案】﹣1
    【解析】解：∵x∈（﹣a，+∞），

    ∴当﹣a＜x＜1﹣a时，y=ln（x+a）＜0，

    当x＞1﹣a时，y=ln（x+a）＞0，

    又（ax+2）ln（x+a）≤0对x∈（﹣a，+∞）恒成立，①若a＞0，y=ax+2与y=ln（x+a）均为定义域上的增函数，

    在x∈（﹣a，+∞）上，可均大于0，不满足题意；②若a=0，则2lnx）≤0对x∈（0，+∞）不恒成立，不满足题意；

    ∴a＜0．

    作图如下：

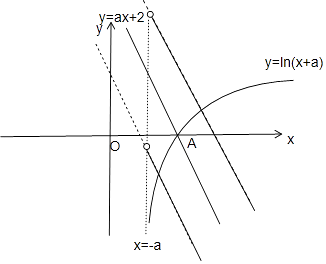
    由图可知，当且仅当方程为y=ln（x+a）的曲线与方程为y=ax+2的直线相交于点A，

    即满足 时，（ax+2）ln（x+a）≤0对x∈（﹣a，+∞）恒成立，

    解方程 得 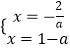，解得a=﹣1．

    所以答案是：﹣1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=log2（ ）﹣x（m为常数）是奇函数．
    （1）判断函数f（x）在x∈（ ，+∞）上的单调性，并用定义法证明你的结论；
    （2）若对于区间[2，5]上的任意x值，使得不等式f（x）≤2x+m恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（x﹣2）|x+a|（a∈R）
    （1）当a=1时，求函数f（x）的单调递增区间；
    （2）当x∈[﹣2，2]时，函数f（x）的最大值为g（a），求g（a）的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=|sinx+cosx|+|sinx﹣cosx|是（ ）
    A.最小正周期为π的奇函数
    B.最小正周期为π的偶函数
    C.最小正周期为 的奇函数
    D.最小正周期为 的偶函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 展开式中，第五项的二项式系数与第三项的二项式系数的比是14：3．
    （1）求n．
    （2）求含x2项的系数．
    （3）求展开式中所有有理项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（x﹣1）|x﹣a|﹣x﹣2a（x∈R）．
    （1）若a=﹣1，求方程f（x）=1的解集；
    （2）若 ，试判断函数y=f（x）在R上的零点个数，并求此时y=f（x）所有零点之和的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】雾霾是人体健康的隐形杀手，爱护环境，人人有责．某环保实验室在雾霾天采用清洁剂处理教室空气质量．实验发现，当在教室释放清洁剂的过程中，空气中清洁剂的含剂浓度y（mg/m3）与时间t（h）成正比；释放完毕后，y与t的函数关系为y=（ ）t﹣a（a为常数），如图，已知当教室的空气中含剂浓度在0.25mg/m3以上时，教室最适合人体活动．根据图中信息，从一次释放清洁剂开始，这间教室有h最适合人体活动．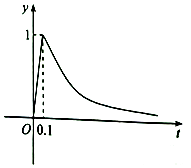

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设f（x）=5|x|﹣ ，则使得f（2x+1）＞f（x）成立的x取值范围是（ ）
    A.（﹣1，﹣ ）
    B.（﹣3，﹣1）
    C.（﹣1，+∞）
    D.（﹣∞，﹣1）∪（﹣ ，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C1： （a＞b＞0）的一个顶点与抛物线C2：x2=4y的焦点重合，F1、F2分别是椭圆C1的左、右焦点，C1的离心率e= ，过F2的直线l与椭圆C1交于M，N两点，与抛物线C2交于P，Q两点．
    （1）求椭圆C1的方程；
    （2）当直线l的斜率k=﹣1时，求△PQF1的面积；
    （3）在x轴上是否存在点A， 为常数？若存在，求出点A的坐标和这个常数；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案