
a,b,c是三条直线,α,β是两个平面,b?α,c?α,则下列命题不成立的是( )
(A)若α∥β,c⊥α,则c⊥β
(B)“若b⊥β,则α⊥β”的逆命题
(C)若a是c在α内的射影,a⊥b,则b⊥c
(D)“若b∥c,则c∥α”的逆否命题
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(九)第二章第六节练习卷(解析版) 题型:选择题
若f(x)=x2-x+a,f(-m)<0,则f(m+1)的值是( )
(A)正数 (B)负数
(C)非负数 (D)不能确定正负
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(一)第一章第一节练习卷(解析版) 题型:选择题
已知集合A={x|x2+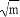 x+1=0},若A∩R=?,则实数m的取值范围是( )
x+1=0},若A∩R=?,则实数m的取值范围是( )
(A)m<4 (B)m>4
(C)0≤m<4 (D)0≤m≤4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷(解析版) 题型:填空题
下列命题中正确的是 .
①若△ABC在平面α外,它的三条边所在的直线分别交平面α于P,Q,R,则P,Q,R三点共线;
②若三条直线a,b,c互相平行且分别交直线l于A,B,C三点,则这四条直线共面;
③空间中不共面的五个点一定能确定10个平面;
④若a不平行于平面α,且a?α,则α内的所有直线与a异面.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷(解析版) 题型:选择题
已知命题:①若点P不在平面α内,A,B,C三点都在平面α内,则P,A,B,C四点不在同一平面内;②两两相交的三条直线在同一平面内;③两组对边分别相等的四边形是平行四边形.其中正确命题的个数是( )
(A)0 (B)1 (C)2 (D)3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:填空题
已知直线l⊥平面α,直线m?平面β,给出下列命题:①α∥β⇒l⊥m.②α⊥β⇒l∥m.③l∥m⇒α⊥β.④l⊥m⇒α∥β,其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:解答题
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.

求证:(1)CM∥平面PAD.
(2)平面PAB⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十五第七章第四节练习卷(解析版) 题型:解答题
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.若M是线段AD的中点,
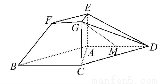
求证:GM∥平面ABFE.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:选择题
长方体的三个相邻面的面积分别为2,3,6,这个长方体的顶点都在同一个球面上,则这个球的表面积为( )
(A) π (B)56π (C)14π (D)64π
π (B)56π (C)14π (D)64π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com