练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系xOy中，抛物线C的顶点是原点O，以x轴为对称轴，且经过点P（1，2）．

    （1）求抛物线C的方程；

    设点A，B在抛物线C上，直线PA，PB分别与y轴交于点M，N，|PM|=|PN|．求直线AB的斜率．

    【答案】(1) (2)-1

    【解析】试题分析：（1）先设抛物线标准方程，代入点坐标可得抛物线方程（2）由|PM|=|PN|得直线PA与PB的倾斜角互补,设直线PA斜率，与抛物线方程联立解得A，同理可得B，最后利用斜率公式求AB斜率

    试题解析：解:(Ⅰ)根据题意,设抛物线C的方程为

    由抛物线C经过点,

    得,

    所以抛物线C的方程为

    (Ⅱ)因为,

    所以,

    所以,

    所以直线PA与PB的倾斜角互补,

    所以

    根据题意,直线AP的斜率存在,设直线AP的方程为:,

    将其代入抛物线C的方程,整理得

    设,则,,

    所以

    以-k替换点A坐标中的k,得

    所以 ,

    所以直线AB的斜率为-1.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数 .
    （I）若曲线 存在斜率为-1的切线，求实数a的取值范围；
    （II）求 的单调区间；
    （III）设函数 ，求证：当 时， 在 上存在极小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校随机调查了80位学生，以研究学生中爱好羽毛球运动与性别的关系，得到下面的数据表：

    爱好

    不爱好

    合计

    男

    20

    30

    50

    女

    10

    20

    30

    合计

    30

    50

    80

    （1）将此样本的频率估计为总体的概率，随机调查了本校的3名学生.设这3人中爱好羽毛球运动的人数为，求的分布列和期望值；

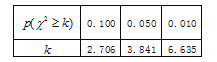
    （2）根据表中数据，能否有充分证据判定爱好羽毛球运动与性别有关联？若有，有多大把握？

    附：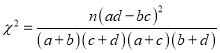

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）若，求曲线 在点处的切线方程；

    （2）当时，讨论函数的单调性。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆：，直线过定点．

    （1）若与圆相切，求直线的方程；

    （2）若点为圆上一点，求的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在三棱柱中， 为正方形， 为菱形， .

    （1）求证：平面⊥平面；

    （2）若是中点，∠是二面角的平面角，求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,四棱锥中, 为正三角形, , 为棱的中点.

    (1)求证:平面平面;

    (2)若直线与平面所成角为,求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数在上存在唯一的满足, 那么称函数是上的“单值函数”.已知函数是上的“单值函数”，当实数取最小值时，函数在上恰好有两点零点，则实数的取值范围是___________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

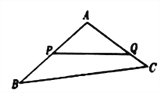
    【题目】如图，某生态园将一块三角形地的一角开辟为水果园，已知角为， 的长度均大于200米，现在边界处建围墙，在处围竹篱笆.

    （1）若围墙、总长度为200米，如何可使得三角形地块面积最大？

    （2）已知竹篱笆长为米， 段围墙高1米， 段围墙高2米，造价均为每平方米100元，求围墙总造价的取值范围.

    查看答案和解析>>

    同步练习册答案