练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图,某房地产公司要在荒地ABCDE上划出一块长方形地面(不改变方位)进行开发.问如何设计才能使开发面积最大,并求出最大面积.(已知BC=210 m,CD=240 m,DE=300 m,EA=180 m)

    思路解析：这是一道规划问题,问题可以转化为在线段AB上求一点,使矩形面积最大的问题.求出直线AB的方程,求解P点坐标是问题的切入点.

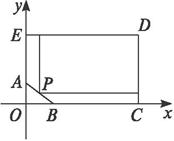
    解：如图,以BC所在直线为x轴,AE所在直线为y轴建立平面直角坐标系xOy,则A(0,60),B(90,0).AB所在的直线方程为+=1,即y=60-x.

    ∴可设P(x,60-x).

    开发面积为S=(300-x)(240-y)=(300-x)·［240-(60-x)］.

    ∴S=-x2+20x+54 000(0＜x＜90.

    当x=-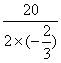=15且y=50时,S取最大值54 150 m2.

    答:矩形顶点P距AE15 m,距BC 50 m时面积最大,最大面积为54 150 m2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

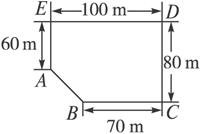
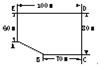    精英家教网某房地产公司要在荒地ABCDE（如图）上划出一块长方形地面（不改变方位）建造一幢八层的公寓楼，问如何设计才能使公寓占地面积最大？并求出最大面积．（精确到1 m2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某房地产公司要在荒地ABCDE（如图所示）上划出一块长方形地面建造一幢公寓，问：如何设计才能使公寓占地面积最大？求出最大面积（尺寸单位：m）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某房地产公司要在荒地ABCDE(如右图)上划出一块长方形地面(不改变方位)进行开发.问如何设计才能使开发面积最大？并求出最大面积.(已知BC=210 m,CD=240 m,DE=300 m,EA=180 m)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某房地产公司要在荒地ABCDE(如图所示)上划出一块长方形地面(不改变方位)建造一幢8层楼公寓，问如何设计才能使公寓占地面积最大？并求出最大面积(精确到1 m2).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

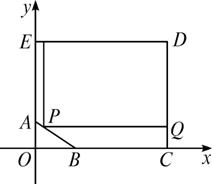
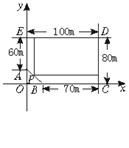
    某房地产公司要在荒地ABCDE(如图所示)上划出一块长方形地面(不改变方位)建造一幢8层楼公寓，问如何设计才能使公寓占地面积最大?并求出最大面积(精确到m2)．

    查看答案和解析>>

    同步练习册答案