
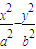 (a>0,b>0)上任意一点P,类似的命题为: .
(a>0,b>0)上任意一点P,类似的命题为: . 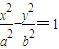 (a>0,b>0)上任意一点P,|PM|•|PN|也必为定值,代入验证即可得到答案.
(a>0,b>0)上任意一点P,|PM|•|PN|也必为定值,代入验证即可得到答案.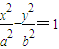 (a>0,b>0)上任意一点P,
(a>0,b>0)上任意一点P,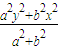 =
=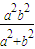
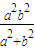


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| a2b2 |
| a2+b2 |
| a2b2 |
| a2+b2 |
查看答案和解析>>
科目:高中数学 来源:2010年湖北省高二上学期期中考试数学试卷 题型:填空题
在平面直角坐标平面内,不难得到“对于双曲线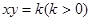 上任意一点
上任意一点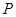 ,若点
,若点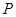 在
在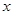 轴、
轴、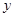 轴上的射影分别为
轴上的射影分别为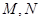 ,则
,则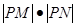 必为定值
必为定值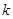 ”。类比于此,对于双曲线
”。类比于此,对于双曲线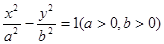 上任意一点
上任意一点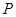 ,类似的命题为
,类似的命题为
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省扬州市江都中学高三第一次调研数学试卷(解析版) 题型:解答题
 (a>0,b>0)上任意一点P,类似的命题为: .
(a>0,b>0)上任意一点P,类似的命题为: .查看答案和解析>>
科目:高中数学 来源:2010年江苏省盐城市东台中学高考数学模拟试卷(一)(解析版) 题型:解答题
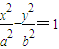 (a>0,b>0)上任意一点P,类似的命题为: .
(a>0,b>0)上任意一点P,类似的命题为: .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com