
【题目】若数列![]() 满足:对于
满足:对于![]() ,都有
,都有![]() (
(![]() 为常数),则称数列
为常数),则称数列![]() 是公差为
是公差为![]() 的“隔项等差”数列.
的“隔项等差”数列.
(Ⅰ)若![]() ,
,![]() 是公差为8的“隔项等差”数列,求
是公差为8的“隔项等差”数列,求![]() 的前
的前![]() 项之和;
项之和;
(Ⅱ)设数列![]() 满足:
满足:![]() ,对于
,对于![]() ,都有
,都有![]() .
.
①求证:数列![]() 为“隔项等差”数列,并求其通项公式;
为“隔项等差”数列,并求其通项公式;
②设数列![]() 的前
的前![]() 项和为
项和为![]() ,试研究:是否存在实数
,试研究:是否存在实数![]() ,使得
,使得![]() 成等比数列(
成等比数列(![]() )?若存在,请求出
)?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)![]() (Ⅱ)① 当
(Ⅱ)① 当![]() 为偶数时,
为偶数时,![]() ,
,
当![]() 为奇数时,
为奇数时,![]() ;②
;②![]()
【解析】
试题(Ⅰ)由新定义知:前![]() 项之和为两等差数列之和,一个是首项为3,公差为8的等差数列前8项和,另一个是首项为17,公差为8的等差数列前7项和,所以前
项之和为两等差数列之和,一个是首项为3,公差为8的等差数列前8项和,另一个是首项为17,公差为8的等差数列前7项和,所以前![]() 项之和
项之和![]() (Ⅱ)①根据新定义知:证明目标为
(Ⅱ)①根据新定义知:证明目标为![]() ,
,![]()
![]() ,相减得
,相减得![]() ,当
,当![]() 为奇数时,依次构成首项为a,公差为2的等差数列,
为奇数时,依次构成首项为a,公差为2的等差数列,![]() , 当
, 当![]() 为偶数时,依次构成首项为2-a,公差为2的等差数列,
为偶数时,依次构成首项为2-a,公差为2的等差数列,![]() ②先求和:当
②先求和:当![]() 为偶数时,
为偶数时, ;当
;当![]() 为奇数时,
为奇数时,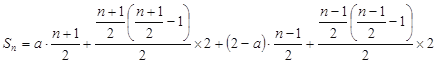
![]() 故当
故当![]() 时,
时,![]() ,
,![]() ,
,![]() , 由
, 由![]() ,则
,则![]() ,解得
,解得![]() .
.
试题解析:(Ⅰ)易得数列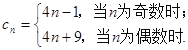
前![]() 项之和
项之和![]()
(Ⅱ)①![]() (
(![]() )(A)
)(A)
![]() (B)
(B)
(B)![]() (A)得
(A)得![]() (
(![]() ).
).
所以,![]() 为公差为2的“隔项等差”数列.
为公差为2的“隔项等差”数列.
当![]() 为偶数时,
为偶数时,![]() ,
,
当![]() 为奇数时,
为奇数时,![]() ;
;
②当![]() 为偶数时,
为偶数时,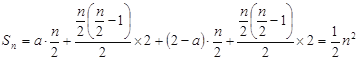 ;
;
当![]() 为奇数时,
为奇数时,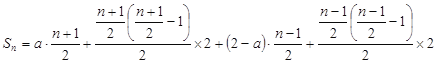
![]() .
.
故当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
由![]() ,则
,则![]() ,解得
,解得![]() .
.
所以存在实数![]() ,使得
,使得![]() 成等比数列(
成等比数列(![]() )
)


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校甲、乙、丙三个年级的学生志愿者人数分别是240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动。
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作,求事件M“抽取的2名同学来自同一年级”发生的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在原点,半径为
的圆心在原点,半径为![]() ,若圆
,若圆![]() 与坐标轴的交点为顶点的四边形是一个面积为
与坐标轴的交点为顶点的四边形是一个面积为![]() 的正方形(记为
的正方形(记为![]() )设点
)设点![]() 在
在![]() 轴的负半轴上,以点
轴的负半轴上,以点![]() 、
、![]() 和点
和点![]() 为顶点的三角形的面积为
为顶点的三角形的面积为![]() .
.
(1)求圆![]() 的半径
的半径![]() 及点
及点![]() 的坐标;
的坐标;
(2)若过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,当线段
两点,当线段![]() 的中点落在正方形
的中点落在正方形![]() 内(包括边界)时,求直线
内(包括边界)时,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期,某公交公司分别推出支付宝和徽信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),统计数据如表l所示:
表1

根据以上数据,绘制了如右图所示的散点图.
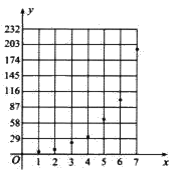
(1)根据散点图判断,在推广期内,![]() (c,d均为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);
(c,d均为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表1中的数据,求y关于x的回归方程,并预测活动推出第8天使用扫码支付的人次;
参考数据:

其中![]()
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: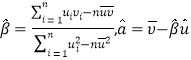 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖南省第九届少数民族传统体育运动会于2018年10月16日至20日在湘西龙山举行.运动会期间,湖南省14个市州和17个民族县市区组成的31个代表团2631人参加,来自土家、苗、瑶、侗、白、维吾尔、壮、回、汉等22个民族的1991名运动员分别参加陀螺、射弩、秋千、高脚、板鞋、蹴球、键球、押加、民族健身操及表演项目比赛,是湖南省历届民族运动会规模最大、规格最高、参赛人数最多的一次.对本次运动会中320名志愿者的年龄抽样调查统计后得到样本频率分布直方图(如图),但是年龄组为![]() 的数据不慎丢失,请完成下面的解答.
的数据不慎丢失,请完成下面的解答.

(1)将频率分布直方图补充完整;
(2)估计本次省民运会中志愿者年龄的众数和中位数(结果保留两位小数);
(3)已知样本容量为16,现在需要从样本中30岁以下的志愿者中抽取2名志愿者谈对本次运动会的感想,求被抽中的志愿者中恰有一名志愿者年龄不小于25岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生会为了解高二年级600名学生课余时间参加中华传统文化活动的情况(每名学生最多参加7场).随机抽取50名学生进行调查,将数据分组整理后,列表如下:
参加场数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
占调查人数的百分比 | 8% | 10% | 20% | 26% | 18% | m% | 4% | 2% |
则以下四个结论中正确的是( )
A.表中m的数值为10
B.估计该年级参加中华传统文化活动场数不高于2场的学生约为108人
C.估计该年级参加中华传统文化活动场数不低于4场的学生约为216人
D.若采用系统抽样方法进行调查,从该校高二600名学生中抽取容量为30的样本,则分段间隔为15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地三角工厂分别位于边长为2的正方形![]() 的两个顶点
的两个顶点![]() 及
及![]() 中点
中点![]() 处.为处理这三角工厂的污水,在该正方形区域内(含边界)与
处.为处理这三角工厂的污水,在该正方形区域内(含边界)与![]() 等距的点
等距的点![]() 处建一个污水处理厂,并铺设三条排污管道
处建一个污水处理厂,并铺设三条排污管道![]() ,记辅设管道总长为
,记辅设管道总长为![]() 千米.
千米.
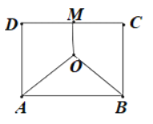
(1)按下列要求建立函数关系式:
(i)设![]() ,将
,将![]() 表示成
表示成![]() 的函数;
的函数;
(ii)设![]() ,将
,将![]() 表示成
表示成![]() 的函数;
的函数;
(2)请你选用一个函数关系,确定污水厂位置,使铺设管道总长最短.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com