
【题目】在一条笔直公路上有A,B两地,甲骑自行车从A地到B地,乙骑着摩托车从B地到A地,到达A地后立即按原路返回,如图是甲乙两人离A地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图象,根据图象解答以下问题:
之间的函数图象,根据图象解答以下问题:
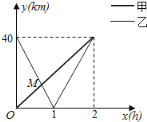
![]() 直接写出
直接写出![]() ,
,![]() 与x之间的函数关系式
与x之间的函数关系式![]() 不必写过程
不必写过程![]() ,求出点M的坐标,并解释该点坐标所表示的实际意义;
,求出点M的坐标,并解释该点坐标所表示的实际意义;
![]() 若两人之间的距离不超过5km时,能够用无线对讲机保持联系,求在乙返回过程中有多少分钟甲乙两人能够用无线对讲机保持联系;
若两人之间的距离不超过5km时,能够用无线对讲机保持联系,求在乙返回过程中有多少分钟甲乙两人能够用无线对讲机保持联系;
![]() 若甲乙两人离A地的距离之积为
若甲乙两人离A地的距离之积为![]() ,求出函数
,求出函数![]() 的表达式,并求出它的最大值.
的表达式,并求出它的最大值.
【答案】(1)M(![]() ,
,![]() ),甲乙经过
),甲乙经过![]() h第一次相遇,此时离A距离
h第一次相遇,此时离A距离![]() km;(2)甲乙两人能够用无线对讲机保持联系;(3)可得f(x)的最大值为f(2)=1600.
km;(2)甲乙两人能够用无线对讲机保持联系;(3)可得f(x)的最大值为f(2)=1600.
【解析】
试题(1)由图形,结合一次函数的解析式的求法,可得所求解析式;再令y甲=y乙,求得M的坐标,进而得到几何意义;
(2)令y甲﹣y乙≤5,解不等式可得x的范围,进而得到所求结论;
(3)运用分段函数的形式写出f(x),再由二次函数的最值的求法,即可得到所求的最大值.
解:(1)y甲=20x,0≤x≤2;y乙=![]() ,
,
令y甲=y乙,可得20x=40﹣40x,解得x=![]() ,
,
进而y甲=y乙=![]() ,即有M(
,即有M(![]() ,
,![]() ),
),
M的坐标表示:甲乙经过![]() h第一次相遇,此时离A距离
h第一次相遇,此时离A距离![]() km;
km;
(2)乙返回过程中,当1<x≤2时,乙与甲相距5km之内,
即y甲﹣y乙≤5,即为20x﹣(40x﹣40)≤5,解得x≥![]() ,即
,即![]() ≤x≤2,
≤x≤2,
则(2﹣![]() )×60=15分钟,甲乙两人能够用无线对讲机保持联系;
)×60=15分钟,甲乙两人能够用无线对讲机保持联系;
(3)f(x)=![]() =
=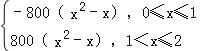
=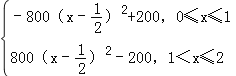 ,
,
当0<x≤1时,f(x)的最大值为f(![]() )=200;
)=200;
当1<x≤2时,f(x)递增,f(2)为最大值,且为1600.
综上可得f(x)的最大值为f(2)=1600.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】某轮船公司的一艘轮船每小时花费的燃料费与轮船航行速度的平方成正比,比例系数为![]() 轮船的最大速度为15海里
轮船的最大速度为15海里![]() 小时
小时![]() 当船速为10海里
当船速为10海里![]() 小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元
小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元![]() 假定运行过程中轮船以速度v匀速航行.
假定运行过程中轮船以速度v匀速航行.
![]() 求k的值;
求k的值;
![]() 求该轮船航行100海里的总费用
求该轮船航行100海里的总费用![]() 燃料费
燃料费![]() 航行运作费用
航行运作费用![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=ex+2x2-3x.
(1)求证:函数f (x)在区间[0,1]上存在唯一的极值点.
(2)当x≥![]() 时,若关于x的不等式f (x)≥
时,若关于x的不等式f (x)≥![]() x2+(a-3)x+1恒成立,试求实数a的取值范围.
x2+(a-3)x+1恒成立,试求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)令![]() ,可将已知三角函数关系
,可将已知三角函数关系![]() 转换成代数函数关系
转换成代数函数关系![]() ,试写出函数
,试写出函数![]() 的解析式及定义域;
的解析式及定义域;
(2)求函数![]() 的最大值;
的最大值;
(3)函数![]() 在区间
在区间![]() 内是单调函数吗?若是,请指出其单调性;若不是,请分别指出其单调递增区间和单调递减区间(不需要证明).
内是单调函数吗?若是,请指出其单调性;若不是,请分别指出其单调递增区间和单调递减区间(不需要证明).
(参考公式:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() ,g(x)=|x﹣2|,则下列结论正确的是( )
,g(x)=|x﹣2|,则下列结论正确的是( )
A.h(x)=f(x)+g(x)是偶函数
B.h(x)=f(x)?g(x)是奇函数
C.h(x)= ![]() 是偶函数
是偶函数
D.h(x)= ![]() 是奇函数
是奇函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆一中为了增强学生的记忆力和辨识力,组织了一场类似《最强大脑》的![]() 赛,
赛,![]() 两队各由4名选手组成,每局两队各派一名选手
两队各由4名选手组成,每局两队各派一名选手![]() ,除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛
,除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛![]() 队选手获胜的概率均为
队选手获胜的概率均为![]() ,且各局比赛结果相互独立,比赛结束时
,且各局比赛结果相互独立,比赛结束时![]() 队的得分高于
队的得分高于![]() 队的得分的概率为( )
队的得分的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com