
【题目】已知![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,
,![]() .设
.设![]() 为线段
为线段![]() 上一点,
上一点,![]() ,有下列条件:
,有下列条件:
①![]() ;②
;②![]() ;③
;③![]() .
.
请从以上三个条件中任选两个,求![]() 的大小和
的大小和![]() 的面积.
的面积.
【答案】![]() ;
;![]() 的面积为1
的面积为1
【解析】
若选①②,则![]() ,
,![]() ,根据余弦定理即可求出
,根据余弦定理即可求出![]() ,结合等腰三角形的性质和三角形的内角和得出
,结合等腰三角形的性质和三角形的内角和得出![]() ,再根据正弦定理求出
,再根据正弦定理求出![]() ,通过三角形内角和关系求得
,通过三角形内角和关系求得![]() ,则
,则![]() ,最后利用三角形面积公式即可求出
,最后利用三角形面积公式即可求出![]() 的面积;
的面积;
若选②③,![]() ,
,![]() ,
,![]() ,可求得
,可求得![]() ,根据余弦定理即可求出
,根据余弦定理即可求出![]() ,三角形的内角和得出
,三角形的内角和得出![]() ,再根据正弦定理求出
,再根据正弦定理求出![]() ,通过三角形内角和关系求得
,通过三角形内角和关系求得![]() ,则
,则![]() ,最后利用三角形面积公式即可求出
,最后利用三角形面积公式即可求出![]() 的面积;
的面积;
若选①③,则![]() ,
,![]() ,由余弦定理可求出
,由余弦定理可求出![]() ,由
,由![]() ,结合等腰三角形的性质和三角形的内角和得出
,结合等腰三角形的性质和三角形的内角和得出![]() ,由三角形内角和关系得出
,由三角形内角和关系得出![]() ,再根据正弦定理求出
,再根据正弦定理求出![]() ,通过三角形内角和关系求得
,通过三角形内角和关系求得![]() ,则
,则![]() ,最后利用三角形面积公式即可求出
,最后利用三角形面积公式即可求出![]() 的面积.
的面积.
(解法一)选①②,则![]() ,
,![]() ,
,
由余弦定理可得:![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,
,
在![]() 中,由正弦定理可得
中,由正弦定理可得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
则在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
(解法二)选②③,∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
由余弦定理可得:![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
在![]() 中,由正弦定理可得
中,由正弦定理可得![]() ,
,
∵![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
则在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
(解法三)选①③,则![]() ,
,![]() ,
,
则:![]() ,
,
由余弦定理可得:![]() ,
,
又![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
在![]() 中,由正弦定理可得
中,由正弦定理可得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
则在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(本小题共l4分)
已知函数f(x)=![]() x +
x +![]() , h(x)=
, h(x)=![]() .
.
(I)设函数F(x)=f(x)一h(x),求F(x)的单调区间与极值;
(Ⅱ)设a∈R,解关于x的方程log4[![]() ]=1og2h(a-x)一log2h (4-x);
]=1og2h(a-x)一log2h (4-x);
(Ⅲ)试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂新购置甲、乙两种设备,分别生产A,B两种产品,为了解这两种产品的质量,随机抽取了200件进行质量检测,得到质量指标值的频数统计表如下:
质量指标值 |
|
|
|
|
|
| 合计 |
A产品频数 | 2 | 6 | a | 32 | 20 | 10 | 80 |
B产品频数 | 12 | 24 | b | 27 | 15 | 6 | n |
产品质量2×2列联表
产品质量高 | 产品质量一般 | 合计 | |
A产品 | |||
B产品 | |||
合计 |
附: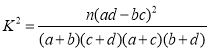
|
|
|
|
|
|
|
|
(1)求a,b,n的值,并估计A产品质量指标值的平均数;
(2)若质量指标值大于50,则说明该产品质量高,否则说明该产品质量一般.请根据频数表完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为质量高低与引入甲、乙设备有关.
的把握认为质量高低与引入甲、乙设备有关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的奇函数![]() ,满足
,满足 ,则下列叙述正确的为( )
,则下列叙述正确的为( )
①存在实数k,使关于x的方程![]() 有7个不相等的实数根
有7个不相等的实数根
②当![]() 时,恒有
时,恒有![]()
③若当![]() 时,
时,![]() 的最小值为1,则
的最小值为1,则![]()
④若关于![]() 的方程
的方程![]() 和
和![]() 的所有实数根之和为零,则
的所有实数根之和为零,则![]()
A.①②③B.①③C.②④D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,左顶点为
,左顶点为![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上的动点,
是椭圆上的动点,![]() 的面积的最大值为
的面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,线段
,线段![]() 的中垂线为
的中垂线为![]() .若直线
.若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系![]() 的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线
的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线![]() (
(![]() 为参数)上每一点的横坐标变为原来的
为参数)上每一点的横坐标变为原来的![]() (纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为
(纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为![]() .
.
(1)求曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,与x轴交于点P,线段AB的中点为M,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明家的晚报在下午![]() 任何一个时间随机地被送到,他们一家人在下午
任何一个时间随机地被送到,他们一家人在下午![]() 任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,
任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,![]() 编号为01,
编号为01,![]() 编号为02,依此类推,
编号为02,依此类推,![]() 编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为
编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为![]()
![]()
7840 1160 5054 3139 8082 7732 5034 3682 4829 4052 |
4201 6277 5678 5188 6854 0200 8650 7584 0136 7655 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com