
分析 先求出n的值,再写出展开式的通项,
(1)根据展开式的通项即可求出二项式系数最大的项,
(2)若第r+1项Tr+1的系数的绝对值最大,得到关于r的不等式组,解得即可.
解答 解:∵M+N-P=4n+2n+5-2n=(2n)2+31•2n=2016,
∴(2n)2+31•2n-2016=0,
∴(2n+63)(2n-32)=0,
∴2n=32,
∴n=5,
∴${(2{x^2}-\frac{1}{x^2})^{10}}$的展开式的通项${T_{r+1}}=C_{10}^r{(2{x^2})^{10-r}}{(-\frac{1}{x^2})^r}={(-1)^r}{2^{10-r}}C_{10}^r{x^{20-4r}}$,
(1)${(2{x^2}-\frac{1}{x^2})^{10}}$的展开式共有11项,二项式系数最大的项为中间项第6项,其值为${T_6}={(-1)^5}{2^5}C_{10}^5=-8064$,
(2)第r+1项Tr+1的系数的绝对值为${A_{r+1}}={2^{10-r}}C_{10}^r$,
若第r+1项Tr+1的系数的绝对值最大,则{$\begin{array}{l}{A_{r+1}}≥{A_r}\\{A_{r+1}}≥{A_{r+2}}\end{array}$,
可得$\frac{8}{3}≤r≤\frac{11}{3}$,又r∈N*,∴r=3,
故系数的绝对值最大的项为${T_4}={(-1)^3}{2^7}C_{10}^3{x^8}=-15360{x^8}$.
点评 本题考查二项展开式的二项式系数的性质;利用二项展开式的通项公式求展开式的特定项.


科目:高中数学 来源: 题型:解答题

| 优分 | 非优分 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 | 50 |
| P(K2≥k2) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 0.46 | 0.71 | 1.32 | 2.07 | 2.71 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}π}}{5}$ | B. | $\frac{{2\sqrt{5}π}}{5}$ | C. | $\frac{{4\sqrt{5}π}}{5}$ | D. | $\frac{{8\sqrt{5}π}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
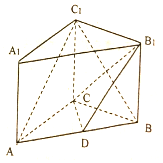 如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点.
如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a、b、c中至少有二个为负数 | B. | a、b、c中至多有一个为负数 | ||
| C. | a、b、c中至多有二个为正数 | D. | a、b、c中至多有二个为负数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.
已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com