
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如下图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | ||
60岁以下 | 140 | ||
合计 | 300 |

(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有97.5%的把握认为潜伏期长短与患者年龄有关:
(3)研究发现,有5种药物对新冠病毒有一定的抑制作用,其中有2种特别有效,现在要通过逐一试验直到把这2种特别有效的药物找出来为止,每一次试验花费的费用是500元,设所需要的试验费用为X,求X的分布列与数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

【答案】(1)平均数为![]() ,“长潜伏者”的人数为
,“长潜伏者”的人数为![]() 人
人
(2)列联表见解析, 有97.5%的把握认为潜伏期长短与年龄有关
(3)分布列见解析,![]()
【解析】
(1)由频率分布直方图可计算出潜伏期的均值,再由频率分布直方图可得“长潜伏者”的频率,从而得人数;
(2)由所给数据计算出![]() 后可得结论;
后可得结论;
(3)由题意知所需要的试验费用X所有可能的取值为1000,1500,2000,分别计算出概率得概率分布列,再由期望公式得期望.
解:(1)平均数![]() ,
,
这500名患者中“长潜伏者”的频率为![]() ,所以“长潜伏者”的人数为
,所以“长潜伏者”的人数为![]() 人.
人.
(2)由题意补充后的列联表如下,
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | 70 | 160 |
60岁以下 | 60 | 80 | 140 |
合计 | 150 | 150 | 300 |
则![]() 的观测值为
的观测值为![]() ,
,
经查表,得![]() ,所以有97.5%的把握认为潜伏期长短与年龄有关.
,所以有97.5%的把握认为潜伏期长短与年龄有关.
(3)由题意知所需要的试验费用X所有可能的取值
为1000,1500,2000,因为![]() ,
,
![]() ,
,
![]() (或
(或![]() )
)
所以X的分布列为
X | 1000 | 1500 | 2000 |
P |
|
|
|
![]() (元).
(元).


科目:高中数学 来源: 题型:
【题目】改编自中国神话故事的动画电影《哪吒之魔童降世》自7月26日首映,在不到一个月的时间,票房收入就超过了38亿元,创造了中国动画电影的神话.小明和同学相约去电影院观看《哪吒之魔童降世》,影院的三个放映厅分别在7:30,8:00,8:30开始放映,小明和同学大约在7:40至8:30之间到达影院,且他们到达影院的时间是随机的,那么他们到达后等待的时间不超过10分钟的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,同比增长率一般是指和去年同期相比较的增长率,环比增长率一般是指和前一时期相比较的增长率.2020年2月29日人民网发布了我国2019年国民经济和社会发展统计公报图表,根据2019年居民消费价格月度涨跌幅度统计折线图,下列说法正确的是( )
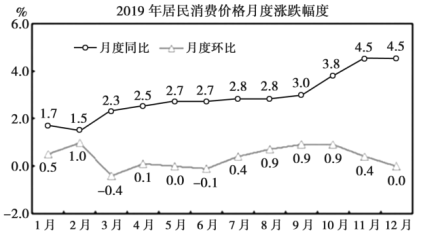
A.2019年我国居民每月消费价格与2018年同期相比有涨有跌
B.2019年我国居民每月消费价格中2月消费价格最高
C.2019年我国居民每月消费价格逐月递增
D.2019年我国居民每月消费价格3月份较2月份有所下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着移动互联网的发展,与餐饮美食相关的手机APP软件层出不穷.现从某市使用A和B两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下.


![]()
![]()
(1)已知抽取的100个使用A款订餐软件的商家中,甲商家的“平均送达时间”为18分钟。现从使用A款订餐软件的商家中“平均送达时间”不超过20分钟的商家中随机抽取3个商家进行市场调研,求甲商家被抽到的概率;
(2)试估计该市使用A款订餐软件的商家的“平均送达时间”的众数及平均数;
(3)如果以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择一款订餐,你会选择哪款?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于由正整数构成的数列![]() ,若对任意
,若对任意![]() ,
,![]() “且
“且![]() ,
,![]() 也是
也是![]() 中的项,则称
中的项,则称![]() 为
为![]() 数列”.设数列
数列”.设数列![]() |满足
|满足![]() ,
,![]() ..
..
(1)请给出一个![]() 的通项公式,使得
的通项公式,使得![]() 既是等差数列也是“
既是等差数列也是“![]() 数列”,并说明理由;
数列”,并说明理由;
(2)根据你给出的通项公式,设![]() 的前
的前![]() 项和为
项和为![]() ,求满足
,求满足![]() 的正整数
的正整数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为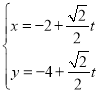 (t为参数),以坐标原点O为极点,以x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,以x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)已知定点![]() ,直线
,直线![]() 与曲线C分别交于P、Q两点,求
与曲线C分别交于P、Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以昆明、玉溪为中心的滇中地区,冬无严寒、夏无酷暑,世界上主要的鲜切花品种在这里都能实现周年规模化生产.某鲜花批发店每天早晨以每支2元的价格从鲜切花生产基地购入某种玫瑰,经过保鲜加工后全部装箱(每箱500支,平均每支玫瑰的保鲜加工成本为1元),然后以每箱2000元的价格整箱出售.由于鲜花的保鲜特点,制定了如下促销策略:若每天下午3点以前所购进的玫瑰没有售完,则对未售出的玫瑰以每箱1200元的价格降价处理.根据经验,降价后能够把剩余玫瑰全部处理完毕,且当天不再购进该种玫瑰,由于库房限制每天最多加工6箱.
(1)若某天该鲜花批发店购入并加工了6箱该种玫瑰,在下午3点以前售出4箱,且被6位不同的顾客购买.现从这6位顾客中随机选取2人赠送优惠卡,则恰好一位是以2000元价格购买的顾客,另一位是以1200元价格购买的顾客的概率是多少?
(2)该鲜花批发店统计了100天内该种玫瑰在每天下午3点以前的销售量![]() (单位:箱),统计结果如下表所示(视频率为概率):
(单位:箱),统计结果如下表所示(视频率为概率):
| 4 | 5 | 6 |
频数 | 30 |
|
|
①估计接下来的一个月(30天)内该种玫瑰每天下午3点以前的销售量不少于5箱的天数是多少?
②若批发店每天在购进5箱数量的玫瑰时所获得的平均利润最大(不考虑其他成本),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com