
【题目】等轴双曲线C的中心在原点,焦点在x轴上,双曲线C与抛物线y2=16x的准线交于A,B两点,|AB|=4 ![]() ,则双曲线C的实轴长为( )
,则双曲线C的实轴长为( )
A.![]()
B.2 ![]()
C.4
D.4 ![]()
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是等比数列,满足a2=6,a3=﹣18,数列{bn}满足b1=2,且{2bn+an}是公差为2的等差数列.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x)﹣x+ ![]() x2(k≥0). (Ⅰ)当k=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
x2(k≥0). (Ⅰ)当k=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x1、x2是一元二次方程4kx2﹣4kx+k+1=0的两个实数根.
(1)是否存在实数k,(2x1﹣x2)(x1﹣2x2)=﹣ ![]() 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由.
(2)求使 ![]() +
+ ![]() ﹣2的值为整数的实数k的整数值.
﹣2的值为整数的实数k的整数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() 是定义在(﹣1,1)上的奇函数,且f(
是定义在(﹣1,1)上的奇函数,且f( ![]() )=
)= ![]() .
.
(1)确定函数f(x)的解析式;
(2)用定义证明f(x)在(﹣1,1)上是增函数;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣2tx+2,g(x)=ex﹣1+e﹣x+1 , 且函数f(x)的图象关于直线x=1对称.
(1)求函数f(x)在区间[0,4]上最大值;
(2)设 ![]() ,不等式h(2x)﹣k2x≥0在x∈[﹣1,1]上恒成立,求实数k的取值范围;
,不等式h(2x)﹣k2x≥0在x∈[﹣1,1]上恒成立,求实数k的取值范围;
(3)设F(x)=f(x)+ag(x)﹣2有唯一零点,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: ![]() =
= 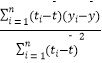 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com