
 ,α和β为锐角;
,α和β为锐角; ;求β;
;求β; )cot
)cot ,满足条件的α和β是否存在?若存在,请求出α和β的值;若不存在,请说明理由.
,满足条件的α和β是否存在?若存在,请求出α和β的值;若不存在,请说明理由. ,
,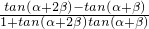 =
= =
=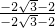 =1
=1 .
. 得
得 +β=
+β= ,
, +β)=
+β)=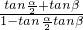 =tan
=tan =
= ,
, )cot
)cot 即tan
即tan tanβ=2-
tanβ=2-
 +tanβ=3-
+tanβ=3- ,
, 和tanβ是一元二次方程x2-(3-
和tanβ是一元二次方程x2-(3- )x+2-
)x+2- =0的两根,
=0的两根, .
. =1,则α=90°与0<α<90°矛盾,舍去;
=1,则α=90°与0<α<90°矛盾,舍去; =2-
=2- ,tanβ=1,
,tanβ=1, 和α+2β=
和α+2β= 化简得到tanβ的值,根据特殊角的三角函数值求出β即可;
化简得到tanβ的值,根据特殊角的三角函数值求出β即可; 两边除以2得到
两边除以2得到 +β=
+β= ,两边去正切值得到正切之和和正切之积的关系,然后再根据tanβ=(2-
,两边去正切值得到正切之和和正切之积的关系,然后再根据tanβ=(2- )cot
)cot 得到正切之和,正切之积的值,利用根与系数的关系写出一个方程,求出方程的解,利用特殊角的三角函数值求出α和β,故存在这样的角度满足条件.
得到正切之和,正切之积的值,利用根与系数的关系写出一个方程,求出方程的解,利用特殊角的三角函数值求出α和β,故存在这样的角度满足条件.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源:2012-2013学年江苏省常州二中高三(上)10月周末数学试卷(文科)(解析版) 题型:填空题
 是1-a和1+a的等比中项,则a+4b的取值范围是 .
是1-a和1+a的等比中项,则a+4b的取值范围是 .查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省菏泽市鄄城实验中学高三(下)双周适应性训练数学试卷4(文科)(解析版) 题型:选择题
 是1-a和1+a的等比中项,则a+4b的取值范围是( )
是1-a和1+a的等比中项,则a+4b的取值范围是( )
 )
)
 )
)查看答案和解析>>
科目:高中数学 来源:2010年全国统一高考数学预测试卷(理科)(解析版) 题型:选择题
 是1-a和1+a的等比中项,则a+4b的取值范围是( )
是1-a和1+a的等比中项,则a+4b的取值范围是( )
 )
)
 )
)查看答案和解析>>
科目:高中数学 来源:2010年全国统一高考数学预测试卷(文科)(解析版) 题型:选择题
 是1-a和1+a的等比中项,则a+4b的取值范围是( )
是1-a和1+a的等比中项,则a+4b的取值范围是( )
 )
)
 )
)查看答案和解析>>
科目:高中数学 来源:2010年河南省许昌市长葛三高高考数学预测试卷(文科)(解析版) 题型:选择题
 是1-a和1+a的等比中项,则a+4b的取值范围是( )
是1-a和1+a的等比中项,则a+4b的取值范围是( )
 )
)
 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com