
四棱锥V-ABCD底面是边长为4的菱形,∠BAD=120°,VA⊥底面ABCD,VA=3,AC与BD交于O,
(1)求点V到CD的距离;
(2)求点V到BD的距离;
(3)作OF⊥VC,垂足为F,证明OF是BD与VC的公垂线段;
(4)求异面直线BD与VC间的距离.
|
解析:用三垂线定理作点到线的垂线 在平面ABCD内作AE⊥CD,E为垂足
∵VA⊥平面ABCD ∴AE为VE在平面ABCD上的射影 ∴VE⊥CD ∴线段VE长为点V到直线CD的距离 ∵∠BAD=120° ∴∠ADC=60° ∴△ACD为正三角形 ∴E为CD中点,AE= ∴VE= (2)∵AO⊥BD ∴由三垂线定理VO⊥BD ∴VO长度为V到直线BD距离 VO= (3)只需证OF⊥BD ∵BD⊥HC,BD⊥VA ∴BD⊥平面VAC ∴BD⊥OF ∴OF为异面直线BD与VC的公垂线 (4)求出OF长度即可 在Rt△VAC中 OC= ∴OF=OC·sin∠ACF=OC· |


科目:高中数学 来源:黄冈中学 高二数学(下册)、考试卷6 直线、平面、简单几何体综合 题型:044
如图,以正四棱锥V-ABCD底面中心O为坐标原点建立直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC的中点,正四棱锥底面边长为2a,高为h.
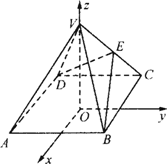
(1)求![]() ;
;
(2)设角∠BCV为α,∠DCV为β,且∠BED是二面角α-VC-β的平面角,求∠BED.
查看答案和解析>>
科目:高中数学 来源:湖北省荆州中学2008高考复习立体几何基础题题库二(有详细答案)人教版 人教版 题型:044
四棱锥V-ABCD底面是边长为4的菱形,∠BAD=120°,VA⊥底面ABCD,VA=3,AC与BD交于O,
(1)求点V到CD的距离;
(2)求点V到BD的距离;
(3)作OF⊥VC,垂足为F,证明OF是BD与VC的公垂线段;
(4)求异面直线BD与VC间的距离.
查看答案和解析>>
科目:高中数学 来源:必修二训练数学北师版 北师版 题型:044
如图所示,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC的中点,正四棱锥底面边长为2a,高为h.求线段BE的长.
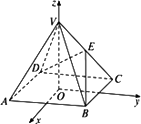
查看答案和解析>>
科目:高中数学 来源:2010-2011年山东省高一第一次阶段检测数学试卷 题型:填空题
如图,在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为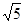 的等腰三角形,则二面角V―AB―C的度数是
。
的等腰三角形,则二面角V―AB―C的度数是
。
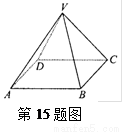
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com