
【题目】已知圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,该动圆圆心
相切,该动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程
的方程
(2)过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点,抛物线在点A的切线与
两点,抛物线在点A的切线与![]() 交于点N,求
交于点N,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ;(2)4.
;(2)4.
【解析】
(1)先设![]() ,动圆半径为
,动圆半径为![]() ,根据题意,列出等量关系,化简整理,即可得出曲线方程;
,根据题意,列出等量关系,化简整理,即可得出曲线方程;
(2)设![]() ,依题意可知,直线
,依题意可知,直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为:
的方程为:![]() ,联立直线与抛物线方程,根据韦达定理,以及弦长公式,表示出
,联立直线与抛物线方程,根据韦达定理,以及弦长公式,表示出![]() ,再表示出过点
,再表示出过点![]() 点的切线方程,求出点
点的切线方程,求出点![]() ,根据点到直线距离公式,以及三角形面积公式,得到
,根据点到直线距离公式,以及三角形面积公式,得到![]() ,即可得出结果.
,即可得出结果.
(1)设![]() ,动圆半径为
,动圆半径为![]() ,因为动圆
,因为动圆![]() 与圆
与圆![]() 外切,
外切,
所以![]() ,
,
又动圆![]() 与直线
与直线![]() 相切,所以由题意可得:
相切,所以由题意可得:![]() ,
,
即![]() ,即
,即![]() ,整理得:
,整理得:![]() ;
;
所以抛物线![]() 的方程为
的方程为![]() .
.
(2)设![]() ,依题意可知,直线
,依题意可知,直线![]() 的斜率存在,
的斜率存在,
故设直线![]() 的方程为:
的方程为:![]() ,
,
联立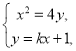 消去
消去![]() 可得,
可得,![]() .
.
则![]() .
.
所以![]()
![]() .
.
由![]() ,得
,得![]() ,
,
所以过![]() 点的切线方程为
点的切线方程为![]() , 又
, 又![]() ,
,
所以切线方程可化为![]() .令
.令![]() ,可得
,可得 ,
,
所以点![]() ,
,
所以点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以![]() ,当
,当![]() 时,等号成立
时,等号成立
所以![]() 面积的最小值为4.
面积的最小值为4.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设双曲线![]() 的左顶点为D,且以点D为圆心的圆
的左顶点为D,且以点D为圆心的圆![]() 与双曲线C分别相交于点A、B,如图所示.
与双曲线C分别相交于点A、B,如图所示.
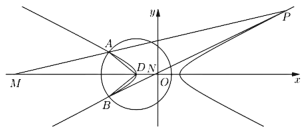
(1)求双曲线C的方程;
(2)求![]() 的最小值,并求出此时圆D的方程;
的最小值,并求出此时圆D的方程;
(3)设点P为双曲线C上异于点A、B的任意一点,且直线PA、PB分别与x轴相交于点M、N,求证:![]() 为定值(其中O为坐标原点).
为定值(其中O为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为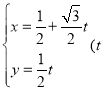 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于![]() 和
和![]() 之间,将测量结果按如下方式分成6组:第1组
之间,将测量结果按如下方式分成6组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
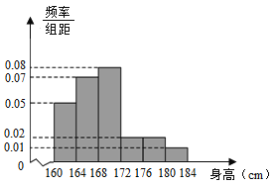
(1)由频率分布直方图估计该校高三年级男生身高的中位数;
(2)在这50名男生身高不低于![]() 的人中任意抽取2人,则恰有一人身高在
的人中任意抽取2人,则恰有一人身高在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇迹之一,其中较为著名的是胡夫金字塔.令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿,还有发生在胡夫金字塔上的数字“巧合”.如胡夫金字塔的底部周长如果除以其高度的两倍,得到的商为3.14159,这就是圆周率较为精确的近似值.金字塔底部形为正方形,整个塔形为正四棱锥,经古代能工巧匠建设完成后,底座边长大约230米.因年久风化,顶端剥落10米,则胡夫金字塔现高大约为( )
A.128.5米B.132.5米C.136.5米D.110.5米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为 (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线![]() 的焦点相同.直线
的焦点相同.直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的一个方向向量为
的一个方向向量为![]() ,求
,求![]() 的面积(其中
的面积(其中![]() 为坐标原点);
为坐标原点);
(3)试问:在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在单位圆O:x2+y2=1上任取一点P(x,y),圆O与x轴正向的交点是A,设将OA绕原点O旋转到OP所成的角为θ,记x,y关于θ的表达式分别为x=f(θ),y=g(θ),则下列说法正确的是( )
A.x=f(θ)是偶函数,y=g(θ)是奇函数
B.x=f(θ)在![]() 为增函数,y=g(θ)在
为增函数,y=g(θ)在![]() 为减函数
为减函数
C.f(θ)+g(θ)≥1对于![]() 恒成立
恒成立
D.函数t=2f(θ)+g(2θ)的最大值为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com