练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    下图是一个几何体的三视图，其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形．

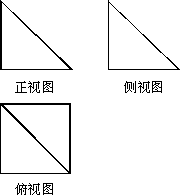
    (1)请画出该几何体的直观图，并求出它的体积；

    (2)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD－A1B1C1D1？如何组拼？

    答案：
    解析：

    　　解：(1)由三视图知，该几何体是有两个侧面垂直于底面的四棱锥，设底面为ABCD，则底面ABCD是边长为6的正方形，高也为6．直观图如图所示，故该几何体的体积V＝×62×6＝72．

    　　(2)由题意，正方体ABCD－A1B1C1D1的体积是原四棱锥体积的3倍，故用3个这样的四棱锥可以拼成一个棱长为6的正方体，其拼法如图所示(均以C1为四棱锥的顶点)．

    　　点评：本题主要考查由几何体的三视图画几何体的直观图，同时考查了同学们对三视图的理解、空间想象能力及推理能力．第(1)问中关键是由正视图和侧视图得出CC1垂直于底面ABCD，而不是C1D垂直于底面ABCD．解决第(2)问的办法是构造一个正方体，从而利用体积关系得出结论．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （07年江西卷文）（12分）

    下图是一个直三棱柱（以为底面）被一平面所截得到的几何体，截面为．已知，，，，．

    （1）设点是的中点，证明：平面；

    （2）求与平面所成的角的大小；

    （3）求此几何体的体积．

    查看答案和解析>>

    科目：高中数学 来源：江西省高考真题 题型：解答题

    下图是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC。已知A1B1=B1C1=1，∠A1B1C1=90°，AA1=4，BB1=2，CC1=3，
    （1）设点O是AB的中点，证明：OC∥平面A1B1C1；
    （2）求二面角B-AC-A1的大小；
    （3）求此几何体的体积．

    查看答案和解析>>

    科目：高中数学 来源：江西省高考真题 题型：解答题

    下图是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC。已知A1B1=B1C1=1，∠A1B1C1=90°，AA1=4，BB1=2，CC1=3，
    （1）设点O是AB的中点，证明：OC∥平面A1B1C1；
    （2）求AB与平面AA1C1C所成的角的大小；
    （3）求此几何体的体积。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=1，∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.

    (1)设点O是AB的中点,证明OC∥平面A1B1C1;

    (2)求AB与平面AA1C1C所成的角的大小;

    (3)求此几何体的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    20. 下图是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC.已知A1B1＝B1C1＝1，∠AlBlC1＝90°，AAl＝4，BBl＝2，CCl＝3.

       （1）设点O是AB的中点，证明：OC∥平面A1B1C1；

       （2）求AB与平面AA1C1C所成的角的大小；

       （3）求此几何体的体积.

    查看答案和解析>>

    同步练习册答案