
【题目】设![]() 是由
是由![]() 个实数组成的有序数组,满足下列条件:①
个实数组成的有序数组,满足下列条件:①![]() ,
,![]() ;②
;②![]() ;③
;③![]() ,
,
![]() .
.
(Ⅰ)当![]() 时,写出满足题设条件的全部
时,写出满足题设条件的全部![]() ;
;
(Ⅱ)设![]() ,其中
,其中![]() ,求
,求![]() 的取值集合;
的取值集合;
(Ⅲ)给定正整数![]() ,求
,求![]() 的个数.
的个数.
【答案】(1) 详见解析;(2) ![]() ; (3)
; (3) ![]()
【解析】试题分析:
(Ⅰ)利用题中所定义的![]() 可得
可得![]() 共有5个可能的值;
共有5个可能的值;
(Ⅱ)利用题意逐一交换元素的位置,讨论可得:![]() 的取值集合为
的取值集合为![]() .
.
(Ⅲ)利用(II)中的方法结合排列组合相关结论可得给定正整数![]() ,求
,求![]() 的个数是
的个数是![]()
试题解析:
(Ⅰ)解:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,共
,共![]() 个.
个.
(Ⅱ)解:首先证明![]() ,且
,且![]() .
.
在③中,令![]() ,得
,得![]() .由①得
.由①得![]() .
.
由②得![]() .
.
在③中,令![]() ,得
,得![]() ,
,
从而![]() .由①得
.由①得![]() .
.
考虑![]() ,即
,即![]() ,
,![]() ,此时
,此时![]() 为最大值.
为最大值.
现交换![]() 与
与![]() ,使得
,使得![]() ,此时
,此时![]() .
.
现将![]() 逐项前移,直至
逐项前移,直至![]() .在前移过程中,显然
.在前移过程中,显然![]() 不变,这一过程称为1次移位.
不变,这一过程称为1次移位.
继续交换![]() 与
与![]() ,使得
,使得![]() ,此时
,此时![]() .
.
现将![]() 逐项前移,直至
逐项前移,直至![]() .在前移过程中,显然
.在前移过程中,显然![]() 不变,执行第2次移位.
不变,执行第2次移位.
依此类推,每次移位![]() 的值依次递减
的值依次递减![]() .经过有限次移位,
.经过有限次移位,![]() 一定可以调整为
一定可以调整为![]() ,
,![]() 交替出现.
交替出现.
注意到![]() 为奇数,所以
为奇数,所以![]() 为最小值.
为最小值.
所以,![]() 的取值集合为
的取值集合为![]() .
.
(Ⅲ)解:由①、②可知,有序数组![]() 中,有
中,有![]() 个
个![]() ,
,![]() 个
个![]() .
.
显然,从![]() 中选
中选![]() 个
个![]() ,其余为
,其余为![]() 的种数共有
的种数共有![]() 种.下面我们考虑这样的数组中有多少个不满足条件③,记该数为
种.下面我们考虑这样的数组中有多少个不满足条件③,记该数为![]() .
.
如果![]() 不满足条件③,则一定存在最小的正整数
不满足条件③,则一定存在最小的正整数![]() ,使得
,使得
(ⅰ)![]() ; (ⅱ)
; (ⅱ)![]() .
.
将![]() 统统改变符号,
统统改变符号,
这一对应![]() 为:
为:![]() ,
,
从而将![]() 变为
变为![]() 个
个![]() ,
,![]() 个
个![]() 组成的有序数组.
组成的有序数组.
反之,任何一个![]() 个
个![]() ,
,![]() 个
个![]() 组成的有序数组
组成的有序数组![]() .由于
.由于![]() 多于
多于![]() 的个数,所以一定存在最小的正整数
的个数,所以一定存在最小的正整数![]() ,使得
,使得![]() .
.
令对应![]() 为:
为:![]() ,
,
从而将![]() 变为
变为![]() 个
个![]() ,
,![]() 个
个![]() 组成的有序数组.
组成的有序数组.
因此,![]() 就是
就是![]() 个
个![]() ,
,![]() 个
个![]() 组成的有序数组的个数.
组成的有序数组的个数.
所以![]() 的个数是
的个数是![]() .
.


科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线
轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线![]() 的参数方程为
的参数方程为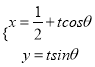 ,(
,( ![]() 为参数,
为参数, ![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线![]()
![]() 上有一点
上有一点![]() (
(![]() ),点
),点![]() 在
在![]() 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线![]() 的右焦点,过点
的右焦点,过点![]() 作双曲线
作双曲线![]() 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为![]() ,
, ![]() ,若平行四边形
,若平行四边形![]() 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装销售公司进行关于消费档次的调查,根据每人月均服装消费额将消费档次分为0-500元;500-1000元;1000-1500元;1500-2000元四个档次,针对![]() 两类人群各抽取100人的样本进行统计分析,各档次人数统计结果如下表所示:
两类人群各抽取100人的样本进行统计分析,各档次人数统计结果如下表所示:
| 0~ 500元 | 500~ 1000元 | 1000~ 1500元 | 1500~ 2000元 |
A类 | 20 | 50 | 20 | 10 |
B类 | 50 | 30 | 10 | 10 |
月均服装消费额不超过1000元的人群视为中低消费人群,超过1000元的视为中高收入人群.
(Ⅰ)从![]() 类样本中任选一人,求此人属于中低消费人群的概率;
类样本中任选一人,求此人属于中低消费人群的概率;
(Ⅱ)从![]() 两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
(Ⅲ)以各消费档次的区间中点对应的数值为该档次的人均消费额,估计![]() 两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).
两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com