
【题目】如图所示,三棱锥V﹣ABC中,VA=VB=AC=BC=2,AB=2 ![]() ,VC=1,线段AB的中点为D.
,VC=1,线段AB的中点为D.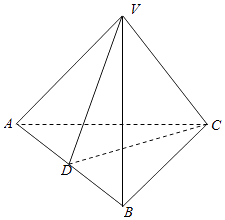
(1)求证:平面VCD⊥平面ABC;
(2)求三棱锥V﹣ABC的体积.
【答案】
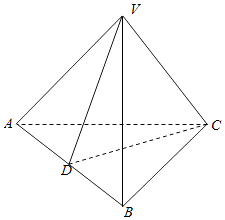
(1)证明:如图所示:
∵VA=VB=2,AB=2 ![]() ,D为AB的中点,
,D为AB的中点,
∴VD⊥AB,VD= ![]() =1.
=1.
同理CD⊥AB,CD=1,CD∩VD=D,∴AB⊥平面VCD.
又∵AB平面ABC,∴平面VCD⊥平面ABC.
(2)解:∵AB⊥平面VCD,
∴三棱锥V﹣ABC的体积等于三棱锥A﹣VCD与B﹣VCD的体积之和.
∵VC=VD=CD=1,
∴△VCD的面积为:
![]() =
= ![]() =
= ![]() ,
,
∴三棱锥V﹣ABC的体积为:
VV﹣ABC= ![]() =
= ![]() =
= ![]() .
.
【解析】1、由已知条件可得VD⊥AB且VD=1,同理可得CD=1由线面垂直的判定定理可得AB⊥平面VCD再由面面垂直的判定定理可得平面VCD⊥平面ABC。
2、由题意可得三棱锥V﹣ABC的体积等于三棱锥A﹣VCD与B﹣VCD的体积之和所以VV﹣ABC= ![]() × S
× S ![]() × A B。
× A B。
【考点精析】通过灵活运用平面与平面垂直的判定,掌握一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为R,导函数f'(x)的图象如图所示,则函数f(x)( ) 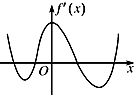
A.无极大值点,有四个极小值点
B.有三个极大值点,两个极小值点
C.有两个极大值点,两个极小值点
D.有四个极大值点,无极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=lnx+ ![]() x2 .
x2 .
(1)求曲线f(x)在x=1处的切线方程;
(2)设P为曲线f(x)上的点,求曲线C在点P处切线的斜率的最小值及倾斜角α的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系.已知曲线C1: ![]() (t为参数),C2:
(t为参数),C2: ![]() (θ为参数). (Ⅰ)化C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(θ为参数). (Ⅰ)化C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若C1上的点P对应的参数为t=﹣ ![]() ,Q为C2上的动点,求线段PQ的中点M到直线C3:ρcosθ﹣
,Q为C2上的动点,求线段PQ的中点M到直线C3:ρcosθ﹣ ![]() ρsinθ=8+2
ρsinθ=8+2 ![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() ,
, ![]() ,
, ![]() 满足|
满足| ![]() |=2,|
|=2,| ![]() +
+ ![]() |=6,|
|=6,| ![]() |=|
|=| ![]() |,且
|,且 ![]() ⊥
⊥ ![]() ,则|
,则| ![]() ﹣
﹣ ![]() |的取值范围为( )
|的取值范围为( )
A.[4,8]
B.[4 ![]() ,8
,8 ![]() ]
]
C.(4,8)
D.(4 ![]() ,8
,8 ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆中心在坐标原点,焦点在x轴上,一个顶点坐标为(2,0),离心率为 ![]() .
.
(1)求这个椭圆的方程;
(2)若这个椭圆左焦点为F1 , 右焦点为F2 , 过F1且斜率为1的直线交椭圆于A、B两点,求△ABF2的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com