
 ,据以往资料统计,第一场比赛组织者可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元.
,据以往资料统计,第一场比赛组织者可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元.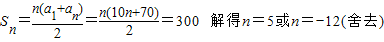
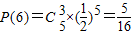 ;
;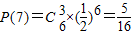



科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)小组赛:经抽签分成甲、乙两组,每组6队进行单循环比赛,以积分及净剩球数取前两名;
(2)半决赛:甲组的第一名与乙组的第二名,乙组的第一名与甲组的第二名作主客场交叉淘汰赛(每两队主客场各赛一场)决出胜者;
(3)决赛:两个胜者参加决赛一场,决出胜负.问全部赛程共需比赛多少场?
查看答案和解析>>
科目:高中数学 来源: 题型:
某次足球赛共12支球队参加,分三个阶段进行:
(1)小组赛:经抽签分成甲、乙两组,每组6队进行单循环比赛,以积分及净剩球数取前两名;
(2)半决赛:甲组第一名与乙组第二名,乙组第一名与甲组第二名作主客场交叉淘汰赛(每两队主客场各赛一场)决出胜者;
(3)决赛:两个胜队参加决赛一场,决出胜负.
问全部赛程共需比赛多少场?
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)小组赛:经抽签分成甲、乙两组,每组6队进行单循环比赛,以积分及净剩球数取前两名;
(2)半决赛:甲组第一名与乙组第二名,乙组第一名与甲组第二名作主客场交叉淘汰赛(每两队主客场各赛一场)决出胜者;
(3)决赛:两个胜队参加决赛一场,决出胜负.
问全部赛程共需比赛多少场?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com