
 如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取到长度为$\sqrt{3}$的线段的概率为( )
如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取到长度为$\sqrt{3}$的线段的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
分析 先求出连接两点所得的所有线段总数,再用列举法求出取到长度为$\sqrt{3}$的线段条数,由此能求出在连接两点所得的所有线段中任取一条线段,取到长度为$\sqrt{3}$的线段的概率.
解答 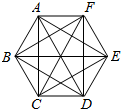 解:∵点A,B,C,D,E,F是边长为1的正六边形的顶点,
解:∵点A,B,C,D,E,F是边长为1的正六边形的顶点,
连接任意两点均可得到一条线段,
∴连接两点所得的所有线段总数n=${C}_{6}^{2}$=15,
∵取到长度为$\sqrt{3}$的线段有:AC、AE、BD、BF、CE、DF,
∴在连接两点所得的所有线段中任取一条线段,取到长度为$\sqrt{3}$的线段的概率为:
p=$\frac{6}{15}$=$\frac{2}{5}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{9}$ | B. | $\frac{11}{9}$ | C. | $\frac{6}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$ | B. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$ | C. | $\frac{{x}^{2}}{12}+\frac{{y}^{2}}{8}=1$ | D. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{8}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
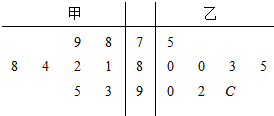 甲、乙两人参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,画出茎叶图如图所示,乙的成绩中有一个数个位数字模糊,在茎叶图中用c表示.(把频率当作概率)
甲、乙两人参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,画出茎叶图如图所示,乙的成绩中有一个数个位数字模糊,在茎叶图中用c表示.(把频率当作概率)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,向量$\overrightarrow{a}$,$\overrightarrow{b}$的位置如图所示,已知|$\overrightarrow{a}$|=|$\overrightarrow{OA}$|=4,|$\overrightarrow{b}$|=|$\overrightarrow{AB}$|=3,且∠AOx=45°,∠OAB=105°,请分别求出向量$\overrightarrow{a}$,$\overrightarrow{b}$的坐标.
在平面直角坐标系xOy中,向量$\overrightarrow{a}$,$\overrightarrow{b}$的位置如图所示,已知|$\overrightarrow{a}$|=|$\overrightarrow{OA}$|=4,|$\overrightarrow{b}$|=|$\overrightarrow{AB}$|=3,且∠AOx=45°,∠OAB=105°,请分别求出向量$\overrightarrow{a}$,$\overrightarrow{b}$的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com