
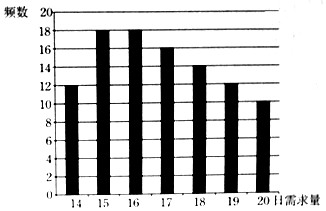
 某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕成本为50元,每个蛋糕的售价为100元,如果当天卖不完,剩余的蛋糕作垃圾处理.现搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率.
某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕成本为50元,每个蛋糕的售价为100元,如果当天卖不完,剩余的蛋糕作垃圾处理.现搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率.分析 (1)当n≥17时,Y=17×(100-50)=850,当n≤16时,Y=100n-17×50=100n-850,由此能求出结果.
(2)①由(1)能求出当天的利润Y关于当天需求量n的函数解析式.②设“当天利润不低于600”为事件A,“当天利润不低于600”等价于“需求量不低于15个,由此能求出当天的利润不低于600元的概率.
(3)求出一天制作16个蛋糕和平均利润和一天制作17个蛋糕的平均利润,从而得到蛋糕店一天应该制作17个生日蛋糕.
解答 解:(1)当n≥17时,Y=17×(100-50)=850,
当n≤16时,Y=100n-17×50=100n-850,
∴当天的利润y=$\left\{\begin{array}{l}{850,n≥17}\\{100n-850,n≤16}\end{array}\right.$.n∈N.
(2)①由(1)得当天的利润Y关于当天需求量n的函数解析式为:
$Y=\left\{\begin{array}{l}100n-850(n≤16)\\ 850(n≥17)\end{array}\right.(n∈N)$
②设“当天利润不低于600”为事件A,由①知,“当天利润不低于600”等价于
“需求量不低于15个”∴$P(A)=1-\frac{12}{100}=\frac{22}{25}$
所以当天的利润不低于600元的概率为:$\frac{22}{25}$
(3)若一天制作16个蛋糕,则平均利润为:
$\overline{x_1}=\frac{1}{100}(600×12+700×18+800×70)=758$;
若一天制作17个蛋糕,则平均利润为:
$\overline{x_2}=\frac{1}{100}(550×12+650×18+750×18+850×52)=760$,
∵$\overline{x_1}<\overline{x_2}$,∴蛋糕店一天应该制作17个生日蛋糕.
点评 本题考查函数解析式、概率、平均数的求法及应用,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | {1,3} | B. | {-3,-1,1} | C. | {-3,1} | D. | {-1,1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}•{(\frac{1}{2})^{n-1}}$ | B. | $\frac{1}{2}•{(\frac{2}{3})^{n-1}}$ | C. | $2•{(\frac{1}{3})^n}-\frac{1}{3}$ | D. | ${(\frac{1}{3})^n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{15}{31}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com