
【题目】已知动圆![]() 过定点
过定点![]() ,且与定直线
,且与定直线![]() 相切.
相切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的任一条直线
的任一条直线![]() 与轨迹
与轨迹![]() 交于不同的两点
交于不同的两点![]() ,试探究在
,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() (异于点
(异于点![]() ),使得
),使得![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1) ![]() ,(2)见解析
,(2)见解析
【解析】
(1)根据抛物线的定义即可得解;
(2)假设存在点![]() 满足题设条件,由题意可得直线
满足题设条件,由题意可得直线![]() 与
与![]() 的斜率互为相反数,即
的斜率互为相反数,即![]() ,设
,设![]() ,
,![]() ,设
,设![]() ,再由直线与抛物线联立,利用韦达定理代入求解即可.
,再由直线与抛物线联立,利用韦达定理代入求解即可.
(1)解法1:依题意动圆圆心![]() 到定点
到定点![]() 的距离与到定直线
的距离与到定直线![]() 的距离相等,
的距离相等,
由抛物线的定义,可得动圆圆心![]() 的轨迹是以
的轨迹是以![]() 为焦点,
为焦点,![]() 为准线的抛物线, 其中
为准线的抛物线, 其中![]() .
.
![]() 动圆圆心
动圆圆心![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
解法2:设动圆圆心![]()
![]() ,依题意:
,依题意:![]() .
.
化简得:![]() ,即为动圆圆心
,即为动圆圆心![]() 的轨迹
的轨迹![]() 的方程
的方程
(2)解:假设存在点![]() 满足题设条件.
满足题设条件.
由![]() 可知,直线
可知,直线![]() 与
与![]() 的斜率互为相反数,
的斜率互为相反数,
即![]() ①
①
直线![]() 的斜率必存在且不为
的斜率必存在且不为![]() ,设
,设![]() ,
,
由![]() 得
得![]() .
.
由![]() ,得
,得![]() 或
或![]() .
.
设![]() ,则
,则![]() .
.
由①式得![]()
![]() ,
,
![]() ,即
,即![]() .
.
消去![]() ,得
,得![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() 存在点
存在点![]() 使得
使得![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】自出生之日起,人的情绪、体力、智力等心理、生理状况就呈周期变化,变化由线为![]() .根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
.根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
(1)请写出小英的体力、情绪和智力节律曲线的函数;
(2)试判断小英在2019年4月22日三种节律各处于什么阶段,当日小英是否适合参加某项体育竞技比赛?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有限集合S中元素的个数记做![]() ,设A,B都为有限集合,给出下列命题:
,设A,B都为有限集合,给出下列命题:
①![]() 的充要条件是
的充要条件是![]()
②![]() 的必要不充分条件是
的必要不充分条件是![]()
③![]() 的充分不必要条件是
的充分不必要条件是![]()
④![]() 的充要条件是
的充要条件是![]()
其中,真命题有( )
A.①②③B.①②C.②③D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x=1与x=2是函数f(x)=aln x+bx2+x的两个极值点.
(1)试确定常数a和b的值;
(2)判断x=1,x=2是函数f(x)的极大值点还是极小值点,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
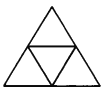
【题目】将边长为![]() 的正三角形利用平行于边的直线剖分为
的正三角形利用平行于边的直线剖分为![]() 个边长为1的小正三角形.图3为
个边长为1的小正三角形.图3为![]() 的情形.证明:存在正整数
的情形.证明:存在正整数![]() ,使得小三角形的顶点中可选出2000
,使得小三角形的顶点中可选出2000![]() 个点,其中,任意三点均不构成正三角形.
个点,其中,任意三点均不构成正三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com