
【题目】已知椭圆C: ![]() 的短轴长为2
的短轴长为2 ![]() ,离心率e=
,离心率e= ![]() ,
,
(1)求椭圆C的标准方程:
(2)若F1、F2分别是椭圆C的左、右焦点,过F2的直线l与椭圆C交于不同的两点A、B,求△F1AB的内切圆半径的最大值.
【答案】
(1)解:由题意可得  …
…
解得 ![]()
故椭圆的标准方程为 ![]()
(2)解:设A(x1,y1),B(x2,y2),设△F1AB的内切圆的半径为R,
因为△F1AB的周长为4a=8, ![]() ,
,
因此 ![]() 最大,R就最大…(6分)
最大,R就最大…(6分) ![]() ,
,
由题意知,直线l的斜率不为零,可设直线l的方程为x=my+1,
由  得(3m2+4)y2+6my﹣9=0,
得(3m2+4)y2+6my﹣9=0,
所以, ![]()
又因直线l与椭圆C交于不同的两点,
故△>0,即(6m)2+36(3m2+4)>0,m∈R,则 ![]()
令 ![]() ,则t≥1,
,则t≥1,  .
.
令  ,由函数的性质可知,函数f(t)在
,由函数的性质可知,函数f(t)在  上是单调递增函数,
上是单调递增函数,
即当t≥1时,f(t)在[1,+∞)上单调递增,
因此有 ![]() ,所以
,所以 ![]() ,
,
即当t=1,m=0时, ![]() 最大,此时
最大,此时 ![]() ,
,
故当直线l的方程为x=1时,△F1AB内切圆半径的最大值为 ![]()
【解析】(1)利用已知条件列出方程组求出a,b,然后求解椭圆的方程.(2)设A(x1 , y1),B(x2 , y2),设△F1AB的内切圆的半径为R,表示出△F1AB的周长与面积,设直线l的方程为x=my+1,联立直线与椭圆方程,利用韦达定理,表示三角形面积,令 ![]() ,利用基本不等式求解面积的最大值,然后求解△F1AB内切圆半径的最大值为
,利用基本不等式求解面积的最大值,然后求解△F1AB内切圆半径的最大值为 ![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆E的一个顶点为A(0,﹣1),焦点在x轴上,若椭圆右焦点到直线x﹣y+2 ![]() =0的距离为3 (Ⅰ)求椭圆E的方程;
=0的距离为3 (Ⅰ)求椭圆E的方程;
(Ⅱ)设直线l:y=kx+m(k≠0)与该椭圆交于不同的两点B,C,若坐标原点O到直线l的距离为 ![]() ,求△BOC面积的最大值.
,求△BOC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=BC=BB1 , AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD. 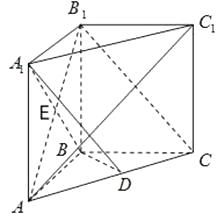
(1)求证:BD⊥平面A1ACC1;
(2)若AB=1,且ACAD=1,求二面角B﹣A1D﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三个函数f(x)=2x+x,g(x)=x﹣1,h(x)=log3x+x的零点依次为a,b,c,则( )
A.a<b<c
B.b<a<c
C.c<a<b
D.a<c<b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知bcosC=(2a﹣c)cosB. (Ⅰ)求B;
(Ⅱ)若c=2,b=3,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图. 
(1)求这100份数学试卷的样本平均分 ![]() 和样本方差s2(同一组中的数据用该组区间的中点值作代表)
和样本方差s2(同一组中的数据用该组区间的中点值作代表)
(2)由直方图可以认为,这批学生的数学总分Z服从正态分布N(μ,σ2),其中μ近似为样本平均数 ![]() ,σ2近似为样本方差s2 . ①利用该正态分布,求P(81<z<119);
,σ2近似为样本方差s2 . ①利用该正态分布,求P(81<z<119);
②记X表示2400名学生的数学总分位于区间(81,119)的人数,利用①的结果,求EX(用样本的分布区估计总体的分布).
附: ![]() ≈19,
≈19, ![]() ≈18,若Z=~N(μ,2),则P(μ﹣σ2),则P(μ﹣σ<Z<μ+σ)=0.6826,P(μ﹣2σ<Z<μ+2σ)=0.9544.
≈18,若Z=~N(μ,2),则P(μ﹣σ2),则P(μ﹣σ<Z<μ+σ)=0.6826,P(μ﹣2σ<Z<μ+2σ)=0.9544.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,BC⊥AC,D,E分别是AB,AC的中点. 
(1)求证:B1C1∥平面A1DE;
(2)求证:平面A1DE⊥平面ACC1A1 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com