练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．作出函数y=cosx|tanx|（0≤x＜$\frac{3π}{2}$，且x≠$\frac{π}{2}$）的图象．

    分析 根据x的取值情况分类讨论，去掉|tanx|中的绝对值符号，转化为分段函数，利用正弦函数的图象即可得解．

    解答 解：∵y=cosx|tanx|=$\left\{\begin{array}{l}{\stackrel{sinx}{-sinx}}&{\stackrel{0≤x＜\frac{π}{2}}{\frac{π}{2}＜x≤π}}\\{-sinx}&{π＜x＜\frac{3π}{2}}\end{array}\right.$，
    ∴函数y=cosx|tanx|（0≤x≤$\frac{3π}{2}$，且x≠$\frac{π}{2}$）的图象如下：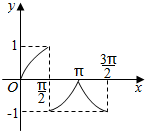
    ．

    点评 本题考查正切函数与正弦函数的图象，确定绝对值符号是关键，考查分类讨论思想，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．函数f（x）=sinx+cosx+sinxcosx，g（x）=mcos（2x-$\frac{π}{6}$）-2m+3（m＞0），若对任意x1∈[0，$\frac{π}{4}$]，存在x2∈[0，$\frac{π}{4}$]，使得g（x1）=f（x2）成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．在△ABC中，a=5，b=4，C=60°，则$\overrightarrow{CB}$•$\overrightarrow{CA}$的值为（　　）
    A．-10B．10C．-10$\sqrt{3}$D．10$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知圆的方程x2+y2-6x-2y-15=0．
    （1）求直线x+2y=0截圆所得的弦长；
    （2）求以原点为中点的弦所在直线方程；
    （3）若点P（x，y）满足圆方程，求$\frac{y-10}{x-8}$的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．函数f（x）=ax2-2x+3在（-∞，1]上是减函数，则实数a的取值范围是（　　）
    A．（-∞，1]B．（0，1]C．[1，+∞）D．[0，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．在空间直角坐标系中，若A（0，1，3），B（-2，1，5），则向量$\overrightarrow{AB}$用坐标表示为（-2，0，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设x，y∈R，则“x，y≥1”是“x2+y2≥2”的（　　）
    A．既不充分也不必要条件B．必要不充分条件
    C．充要条件D．充分不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．在△ABC中，A、B、C的对边分别为a，b，c，已知A≠$\frac{π}{2}$，且3sinAcosB+$\frac{1}{2}$bsin2A=3sinC．
    （I）求a的值；
    （Ⅱ）若A=$\frac{2π}{3}$，求△ABC周长的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

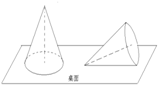    9．用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥，放在水平桌面上，被一阵风吹倒，如图，则它的最高点到桌面的距离为5$\sqrt{3}$cm．

    查看答案和解析>>

    同步练习册答案