练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下面给出的关系式中正确的个数是（ ）
    ① =
    ② =
    ③ 2=| |2
    ④（ ） = （ ）
    ⑤| |≤ ．
    A.0
    B.1
    C.2
    D.3

    【答案】D
    【解析】解：① =0，因此不正确；
    ② = ，满足交换律，正确；
    ③ 2=| |2 ， 正确；
    ④由于 与 不一定共线，因此（ ） = （ ）不正确；
    ⑤由向量的数量积的运算性质即可得出：| |≤ ．
    综上可得：只有②③⑤正确．
    故选：D．
    ① =0，即可判断出；
    ②向量的数量积运算满足交换律；
    ③ 2=| |2 ， 不同的记法；
    ④由于 与 不一定共线，可知（ ） = （ ）不正确；
    ⑤由向量的数量积的运算性质即可得出．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】将甲、乙两颗骰子先后各抛一次，a、b分别表示抛掷甲、乙两颗骰子所出现的点数﹒图中三角形阴影部分的三个顶点为（0，0）、（4，0）和（0，4）．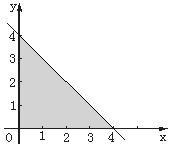

    （1）若点P（a，b）落在如图阴影所表示的平面区域（包括边界）的事件记为A，求事件A的概率；
    （2）若点P（a，b）落在直线x+y=m（m为常数）上，且使此事件的概率P最大，求m和P的值﹒

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，AD=CD=2AB=2，PA⊥AD，AB∥CD，CD⊥AD，E为PC的中点，且DE=EC．

    （1）求证：PA⊥面ABCD；
    （2）设PA=a，若平面EBD与平面ABCD所成锐二面角θ∈（ ， ），求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2+ax+6．
    （1）当a=5时，解不等式f（x）＜0；
    （2）若不等式f（x）＞0的解集为R，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和Sn满足Sn= an+n﹣3．
    （1）求证：数列{an﹣1}是等比数列，并求{an}的通项公式；
    （2）令cn=log3（a1﹣1）+log3（a2﹣1）+…+log3（an﹣1），对任意n∈N*， + +…+ ＜k都成立，求k的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：（x﹣1）2+（y﹣2）2=25及直线l：（2m+1）x+（m+1）y=7m+4．（m∈R）
    （1）证明：不论m取什么实数，直线l与圆C恒相交；
    （2）求直线l与圆C所截得的弦长的最短长度及此时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】两条平行直线和圆的位置关系定义为：若两条平行直线和圆有四个不同的公共点，则称两条平行线和圆“相交”；若两平行直线和圆没有公共点，则称两条平行线和圆“相离”；若两平行直线和圆有一个、两个或三个不同的公共点，则称两条平行线和圆“相切”．已知直线l1：2x﹣y+a=0，l2：2x﹣y+a2+1=0和圆：x2+y2+2x﹣4=0相切，则a的取值范围是（ ）
    A.a＞7或a＜﹣3
    B.
    C.﹣3≤a≤一 或 ≤a≤7
    D.a≥7或a≤﹣3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设P是椭圆 上一点，M、N分别是两圆：（x+4）2+y2=1和（x﹣4）2+y2=1上的点，则|PM|+|PN|的最小值、最大值的分别为（ ）
    A.9，12
    B.8，11
    C.8，12
    D.10，12

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数
    （1）求函数f（x）的最小正周期和函数的单调递增区间；
    （2）已知△ABC中，角A，B，C的对边分别为a，b，c，若 ，求AB．

    查看答案和解析>>

    同步练习册答案