
【题目】已知函数f(x)= ![]() ;
;
(1)若f(x)的定义域为 (-∞,+∞), 求实数a的范围;
(2)若f(x)的值域为 [0, +∞), 求实数a的范围
科目:高中数学 来源: 题型:
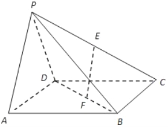
【题目】在四棱锥中![]() ,底面
,底面![]() 是正方形,侧面
是正方形,侧面![]() 底面
底面![]() ,且
,且![]() ,分别为
,分别为![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,若存在,请求出点
,若存在,请求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2-4|x|-5.
(Ⅰ)画出y=f(x)的图象;
(Ⅱ)设A={x|f(x)≥7},求集合A;
(Ⅲ)方程f(x)=k+1有两解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验.为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.
分数 |
|
|
|
|
|
甲班频数 | 5 | 6 | 4 | 4 | 1 |
一般频数 | 1 | 3 | 6 | 5 | 5 |
(1)由以下统计数据填写下面![]() 列联表,并判断能否在犯错误的额概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
列联表,并判断能否在犯错误的额概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附:![]() ,其中
,其中![]() .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中,记成绩不优良的乙班人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下的对应数据:
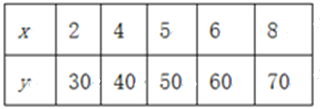
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() =
=![]() x+
x+![]() ;
;
(参考公式:用最小二乘法求线性回归方程系数公式 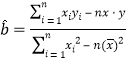 ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为![]() ,答对文科题的概率均为
,答对文科题的概率均为![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com