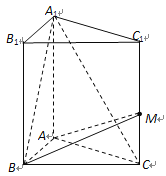
[题目]直三棱柱中.底面为等腰直角三角形. . . . 是侧棱上一点.设．(1) 若.求的值,(2) 若.求直线与平面所成的角．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】直三棱柱中，底面为等腰直角三角形，，，，是侧棱上一点，设．

(1) 若，求的值；

(2) 若，求直线与平面所成的角．

【答案】（1）（2）

【解析】试题分析：（1）以为坐标原点，以射线、、分别为、、轴建立空间直角坐标系，求出，，利用，求出的值；（2）求出直线的方向向量与平面的法向量，求出向量的夹角的余弦值可得结果.

试题解析：（1）以为坐标原点，以射线、、分别为、、轴建立空间直角坐标系，如图所示，

则,，，

，

由得，即

解得．

(2) 解法一：此时

设平面的一个法向量为

由得

所以

设直线与平面所成的角为

则

所以直线与平面所成的角为

解法二：联结，则，

，平面

平面

所以是直线与平面所成的角；

在中，

所以

所以直线与平面所成的角为

练习册系列答案

学练案自主读本系列答案

初中学生学业考试手册系列答案

初中学业考试复习学与练指导丛书系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】设直线与圆交于M、N两点，且M、N关于直线对称．

（1）求m，k的值；

（2）若直线与圆C交P，Q两点，是否存在实数a使得OP⊥OQ，如果存在，求出a的值；如果不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设点为椭圆的左焦点，直线被椭圆截得弦长为．

（1）求椭圆的方程；

（2）圆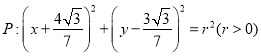与椭圆交于两点，为线段上任意一点，直线交椭圆于两点为圆的直径，且直线的斜率大于，求的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知命题p：x∈A，且A={x|a﹣1＜x＜a+1}，命题q：x∈B，且B={x|x2﹣4x+3≥0}

（Ⅰ）若A∩B=，A∪B=R，求实数a的值；

（Ⅱ）若p是q的充分条件，求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】给出以下四个命题：
①若＜＜0，则 + ＞2；
②若a＞b，则am2＞bm2；
③在△ABC中，若sinA=sinB，则A=B；
④任意x∈R，都有ax2﹣ax+1≥0，则0＜a≤4．
其中是真命题的有（）
A.①②
B.②③
C.①③
D.③④

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在等比数列{an}中，a2=6，a2+a3=24，在等差数列{bn}中，b1=a1 ， b3=﹣10．
（1）求数列{an}的通项公式；
（2）求数列{bn}的前n项和Sn ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某条公共汽车线路收支差额与乘客量的函数关系如图所示（收支差额车票收入支出费用），由于目前本条线路亏损，公司有关人员提出了两条建议：建议(Ⅰ)不改变车票价格，减少支出费用；建议(Ⅱ)不改变支出费用，提高车票价格，下面给出的四个图形中，实线和虚线分别表示目前和建议后的函数关系，则

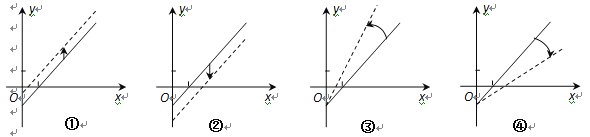
A. ①反映了建议（Ⅱ），③反映了建议（Ⅰ）

B. ①反映了建议（Ⅰ），③反映了建议（Ⅱ）

C. ②反映了建议（Ⅰ），④反映了建议（Ⅱ）

D. ④反映了建议（Ⅰ），②反映了建议（Ⅱ）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知某渔船在渔港O的南偏东60°方向，距离渔港约160海里的B处出现险情，此时在渔港的正上方恰好有一架海事巡逻飞机A接到渔船的求救信号，海事巡逻飞机迅速将情况通知了在C处的渔政船并要求其迅速赶往出事地点施救．若海事巡逻飞机测得渔船B的俯角为68.20°，测得渔政船C的俯角为63.43°，且渔政船位于渔船的北偏东60°方向上．

（Ⅰ）计算渔政船C与渔港O的距离；

（Ⅱ）若渔政船以每小时25海里的速度直线行驶，能否在3小时内赶到出事地点？

（参考数据：sin68.20°≈0.93，tan68.20°≈2.50，shin63.43°≈0.90，tan63.43°≈2.00， ≈3.62， ≈3.61）