【题目】用数字0，1，2，3，4组成没有重复数字且至少有两个数字是偶数的四位数，则这样的四位数的个数为（ ）
A.64B.72C.96D.144
【答案】C
【解析】
由题意把四位数分为含有3个偶数与2个偶数两类,每一类要考虑特殊元素0的安排情况,利用排列组合的应用可分别求出每类四位数的个数,相加即可.
根据题意,数字0，1, 2, 3, 4中有2个奇数,3个偶数.
若组成的四位数要求至少有两个数字是偶数,则四位数中含有2个或3个偶数,分2种情况讨论:
①四位数中含有3个偶数，1个奇数，因为0不能在首位,有3种情况,选取一个奇数有
种，与另两个偶数安排在其他三个位置，有
种情况，
则有
个符合条件的四位数;
②四位数中含有2个偶数,2个奇数;若偶数中有0,在2、4中选出1个偶数,有种取法,其中0不能在首位,有3种情况，将其他3个数全排列,
安排在其他三个位置,有种情况,则有
个符合条件的四位数；若偶数中没有0,将其他4个数全排列,有
个符合条件的四位数；
则一共有36+36+24=96个符合条件的四位数.
故选：C
科目：高中数学 来源： 题型：
【题目】已知定义在R上的偶函数f（x）在（﹣∞，0]上单调递增，且f（﹣1）＝﹣1.若f（x﹣1）+1≥0，则x的取值范围是_____；设函数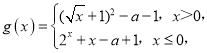
若方程f（g（x））+1＝0有且只有两个不同的实数解，则实数a的取值范围为_____.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）
.
（1）若x＝1是函数f（x）的一个极值点，求k的值及f（x）单调区间；
（2）设g（x）＝（x+1）ln（x+1）+f（x），若g（x）在[0，+∞）上是单调增函数，求实数k的取值范围；
（3）证明：当p＞0，q＞0及m＜n（m，n∈N*）时，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一饮料店制作了一款新饮料，为了进行合理定价先进行试销售，其单价
（元）与销量
（杯）的相关数据如下表：
单价 | 8.5 | 9 | 9.5 | 10 | 10.5 |
销量 | 120 | 110 | 90 | 70 | 60 |
（1）已知销量与单价具有线性相关关系，求关于的线性回归方程；
（2）若该款新饮料每杯的成本为8元，试销售结束后，请利用（1）所求的线性回归方程确定单价定为多少元时，销售的利润最大？（结果四舍五入保留到整数）
附：线性回归方程
中斜率和截距最小二乗法估计计算公式：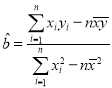
，
，
，
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
