
【题目】已知函数![]() ,
,![]() (
(![]() ,
,![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若对任意![]() 在
在![]() 上总存在两个不同的
上总存在两个不同的![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]() 单调递减区间是
单调递减区间是![]() ;当
;当![]() 时,
时,![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(2)
;(2)![]() .
.
【解析】
试题分析: (1)首先求出函数的导数,然后根据导数的正负解出不等式得到函数的单调区间;(2)求出函数![]() 的导数
的导数![]() ,由
,由![]() 的正负判断函数的单调性并求出函数在
的正负判断函数的单调性并求出函数在![]() 上的值域,当
上的值域,当![]() 时, 不合题意; 当
时, 不合题意; 当![]() 时,判断极值点
时,判断极值点![]() 与端点e的关系,分为
与端点e的关系,分为![]() 时,不合题意;
时,不合题意;![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,又
上单调递增,又![]() 在
在![]() 上恒成立, 欲使对任意的
上恒成立, 欲使对任意的![]() 在
在![]() 上总存在两个不同的
上总存在两个不同的![]() ,使
,使![]() 成立,则需满足
成立,则需满足![]() ,即
,即![]() .
.
试题解析:(1)![]() ,
,![]() .
.
1)当![]() ,
,![]() ;
;
2)当![]() ,令
,令![]() ,
,![]() ;
;
综上:当![]() 时,
时,![]() 的单调递减区间是
的单调递减区间是![]() ;
;
当![]() 时,
时,![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
(2)∵![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 内递增,在
内递增,在![]() 内递减.又∵
内递减.又∵![]() ,
,![]() ,
,![]() ,
,
∴函数![]() 在
在![]() 内的值域为
内的值域为![]() .
.
由![]() ,得
,得![]() .
.
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,不合题意;
上单调递减,不合题意;
②当![]() 时,令
时,令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() .
.
i)当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,不合题意;
上单调递减,不合题意;
ii)当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
令![]() ,
,![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
∴![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,则
,则![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() ,∴
,∴![]() ,∴
,∴![]() ,即
,即![]() .
.
∴当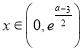 时,
时,![]()
![]() ,
,
且![]() 在
在![]() 上连续.
上连续.
欲使对任意的![]() 在
在![]() 上总存在两个不同的
上总存在两个不同的![]() ,
,
使![]() 成立,则需满足
成立,则需满足![]() ,即
,即![]() .
.
又∵![]() ,∴
,∴![]() ,
,
∴![]() .综上所述,
.综上所述,![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】已知甲乙两名篮球运动员每场比赛得分的原始记录用如下茎叶图表示:
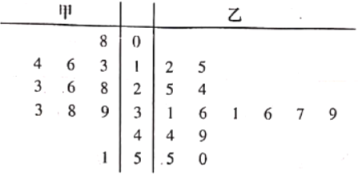
(1)按从小到大的顺序写出甲运动员的得分;
(2)分别求甲乙运动员得分的中位数;
(3)估计乙运动员在一场比赛中得分落在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如表:
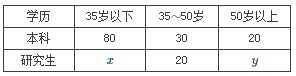
(1)用分层抽样的方法在![]() 岁年龄段的专业技术人员中抽取一个容量为
岁年龄段的专业技术人员中抽取一个容量为![]() 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取![]() 人,求至少有
人,求至少有![]() 人的学历为研究生的概率;
人的学历为研究生的概率;
(2)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取![]() 个人,其中
个人,其中![]() 岁以下
岁以下![]() 人,
人,![]() 岁以上
岁以上![]() 人,再从这
人,再从这![]() 个人中随机抽取出
个人中随机抽取出![]() 人,此人的年龄为
人,此人的年龄为![]() 岁以上的概率为
岁以上的概率为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点![]() ,
,![]() ,动点
,动点![]() 与
与![]() 两点连线的斜率
两点连线的斜率![]() 满足
满足![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)![]() 是曲线
是曲线![]() 与
与![]() 轴正半轴的交点,曲线
轴正半轴的交点,曲线![]() 上是否存在两点
上是否存在两点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了教职工的住房问题,计划征用一块土地盖一幢总建筑面积为![]() 的宿舍楼(每层的建筑面积相同).已知土地的征用费为
的宿舍楼(每层的建筑面积相同).已知土地的征用费为![]() 元
元![]() ,土地的征用面积为第一层的
,土地的征用面积为第一层的![]() 倍,经工程技术人员核算,第一层的建筑费用相同都为400元
倍,经工程技术人员核算,第一层的建筑费用相同都为400元![]() ,以后每增高一层,其建筑费用就增加50元
,以后每增高一层,其建筑费用就增加50元![]() .试设计这幢宿舍楼的楼高层数,使总费用最少,并求出其最少费用.(总费用为建筑费用和征地费用之和).
.试设计这幢宿舍楼的楼高层数,使总费用最少,并求出其最少费用.(总费用为建筑费用和征地费用之和).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在常数![]() ,使得数列
,使得数列![]() 满足:若
满足:若![]() 是数列
是数列![]() 中的一项,则
中的一项,则![]() 也是数列
也是数列![]() 中的一项,称数列
中的一项,称数列![]() 为“兑换数列”,常数
为“兑换数列”,常数![]() 是它的“兑换系数”.
是它的“兑换系数”.
(1)若数列:![]()
![]() 是“兑换系数”为
是“兑换系数”为![]() 的“兑换数列”,求
的“兑换数列”,求![]() 和
和![]() 的值;
的值;
(2)已知有穷等差数列![]() 的项数是
的项数是![]()
![]() ,所有项之和是
,所有项之和是![]() ,求证:数列
,求证:数列![]() 是“兑换数列”,并用
是“兑换数列”,并用![]() 和
和![]() 表示它的“兑换系数”;
表示它的“兑换系数”;
(3)对于一个不小于3项,且各项皆为正整数的递增数列![]() ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com