
【题目】由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“a·b=b·a”;
②“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”;
③“t≠0,mt=ntm=n”类比得到“c≠0,a·c=b·ca=b”;
④“|m·n|=|m|·|n|”类比得到“|a·b|=|a|·|b|”;
⑤“(m·n)t=m(n·t)”类比得到“(a·b)·c=a(b·c)”;
⑥“![]() ”类比得到
”类比得到![]() .以上的式子中,类比得到的结论正确的是________.
.以上的式子中,类比得到的结论正确的是________.
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】两台车床加工同一种机械零件如下表:
分类 | 合格品 | 次品 | 总计 |
第一台车床加工的零件数 | 35 | 5 | 40 |
第二台车床加工的零件数 | 50 | 10 | 60 |
总计 | 85 | 15 | 100 |
从这100个零件中任取一个零件,求:
(1)取得合格品的概率;
(2)取得零件是第一台车床加工的合格品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)在(0, ![]() )上处处可导,若[f(x)﹣f′(x)]tanx﹣f(x)<0,则( )
)上处处可导,若[f(x)﹣f′(x)]tanx﹣f(x)<0,则( )
A.![]() 一定小于
一定小于 ![]()
B.![]() 一定大于
一定大于 ![]()
C.![]() 可能大于
可能大于 ![]()
D.![]() 可能等于
可能等于 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱柱ABCD﹣A1B1C1D1的底面ABCD为正方形,AA1⊥AC,M、N分别为棱AA1、CC1的中点.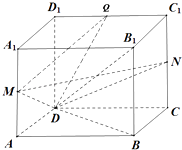
(1)求证:直线MN⊥平面B1BD;
(2)已知AA1=AB,AA1⊥AB,取线段C1D1的中点Q,求二面角Q﹣MD﹣N的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C与椭圆E: ![]() 共焦点,并且经过点
共焦点,并且经过点 ![]() ,
,
(1)求椭圆C的标准方程;
(2)在椭圆C上任取两点P、Q,设PQ所在直线与x轴交于点M(m,0),点P1为点P关于轴x的对称点,QP1所在直线与x轴交于点N(n,0),探求mn是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的镀锌铁皮材料ABCD,上沿DC为圆弧,其圆心为A,圆半径为2米,AD⊥AB,BC⊥AB,且BC=1米。现要用这块材料裁一个矩形PEAF(其中P在圆弧DC上、E在线段AB上,F在线段AD上)做圆柱的侧面,若以PE为母线,问如何裁剪可使圆柱的体积最大?其最大值是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是椭圆E:![]() +y2=1上的任意一点,F1,F2是它的两个焦点,O为坐标原点,动点Q满足
+y2=1上的任意一点,F1,F2是它的两个焦点,O为坐标原点,动点Q满足![]() .
.
(1)求动点Q的轨迹方程;
(2)若已知点A(0,-2),过点A作直线l与椭圆E相交于B,C两点,求△OBC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心在
的圆心在![]() 轴上,并且过
轴上,并且过![]() 两点.
两点.
(1)求圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,那么以
两点,那么以![]() 为直径的圆能否经过原点,若能,请求出直线
为直径的圆能否经过原点,若能,请求出直线![]() 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com