点P为圆O:x2+y2=a2(a>0)上一动点,PD⊥x轴于D点,记线段PD的中点M的运动轨迹为曲线C.
(I)求曲线C的方程;
(II)若动直线l与曲线C交于A、B两点,当△OAB(O是坐标原点)面积取得最大值,且最大值为1时,求a的值.
【答案】
分析:(Ⅰ)确定P,M坐标之间的关系,利用P是圆上的动点,代入x
2+y
2=a
2,即可得曲线C的方程;
(Ⅱ)分类讨论:①当l斜率不存在时,可得S
△OAB最大值为
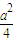
;②当l斜率存在时,表示出三角形的面积,利用基本不等式,可得S
△OAB的最大值为
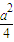
,由已知得
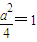
,从而可求a的值.
解答:解:(Ⅰ)设P(x
,y
),M(x,y),由
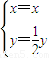
,得
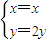
,…(2分)
代入x
2+y
2=a
2,得
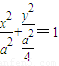
.…(4分)
(Ⅱ)①当l斜率不存在时,设x=t,由已知得-a<t<a,
由

,得
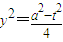
所以
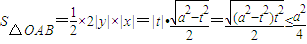
,
当且仅当t
2=a
2-t
2,即
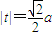
时,等号成立.
此时S
△OAB最大值为
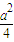
.…(5分)
②当l斜率存在时,设其方程为y=kx+m,
由
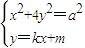
,消去y整理得(4k
2+1)x
2+8kmx+4m
2-a
2=0,
△=(8km)
2-4(4k
2+1)(4m
2-a
2)=4[4k
2+a
2-4m
2]
由△>0,得4k
2a
2+a
2-4m
2>0①
设A(x
1,y
1),B(x
2,y
2),则
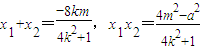
②…(7分)
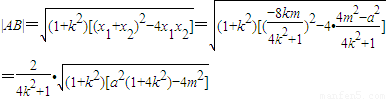
③
原点到直线l距离为
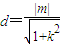
,④…(9分)
由面积公式及③④得
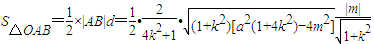
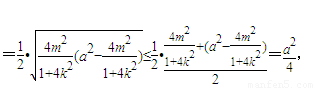
…(11分)
综合①②,S
△OAB的最大值为
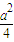
,由已知得
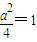
,所以 a=2.…(12分)
点评:本题考查代入法求轨迹方程,考查三角形面积的计算,考查分类讨论的数学思想,考查基本不等式的运用,正确表示三角形的面积是关键.

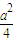 ;②当l斜率存在时,表示出三角形的面积,利用基本不等式,可得S△OAB的最大值为
;②当l斜率存在时,表示出三角形的面积,利用基本不等式,可得S△OAB的最大值为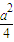 ,由已知得
,由已知得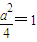 ,从而可求a的值.
,从而可求a的值.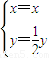 ,得
,得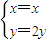 ,…(2分)
,…(2分)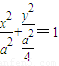 .…(4分)
.…(4分) ,得
,得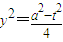
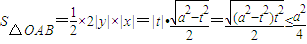 ,
,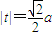 时,等号成立.
时,等号成立.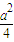 .…(5分)
.…(5分)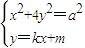 ,消去y整理得(4k2+1)x2+8kmx+4m2-a2=0,
,消去y整理得(4k2+1)x2+8kmx+4m2-a2=0,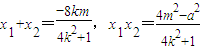 ②…(7分)
②…(7分)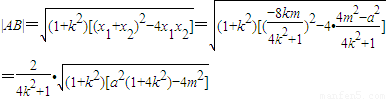 ③
③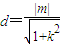 ,④…(9分)
,④…(9分)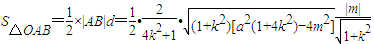
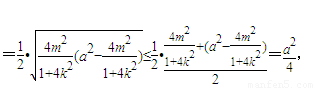 …(11分)
…(11分)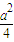 ,由已知得
,由已知得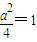 ,所以 a=2.…(12分)
,所以 a=2.…(12分)

 (2011•武昌区模拟)如图,已知点P是圆C:x2+(y-2
(2011•武昌区模拟)如图,已知点P是圆C:x2+(y-2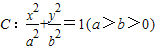 的左焦点F及点A(0,b),原点O到直线FA的距离为
的左焦点F及点A(0,b),原点O到直线FA的距离为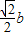 .
.